Graphische Darstellung bei Funktionen mit mehreren Veränderlichen

Inhaltsverzeichnis zum Thema

• Funktionen mit mehreren Veränderlichen
• Flächen im Raum
• Ebenen im Raum
• Paraboloid
• Hyperbolisches Paraboloid
• Höhenlinien
• Isoquanten

Funktionen mit mehreren Veränderlichen

Wir schauen uns hier Funktionen $f$ mit zwei Veränderlichen an, also $z=f(x;y)$.

Den Funktionsgraphen einer solchen Funktion kannst du auf verschiedene Arten darstellen:

• Flächen im Raum: Du wirst im Folgenden zum Beispiel ein Paraboloid, sozusagen eine Parabel im Dreidimensionalen kennenlernen.
• Höhenlinien
• Isoquanten

Flächen im Raum

Wie du bereits gesehen hast, sieht eine Funktion mit zwei Veränderlichen so aus $z=f(x;y)$. Du erhältst also Punkte $(x|y|z)$ im dreidimensionalen Raum. Wenn du diese miteinander verbindest, erhältst du eine Fläche im Raum.

Hierfür schauen wir uns Beispiele an.

Ebenen im Raum

Betrachte die Funktion $f$ mit $f(x;y)=x-y$. Du erhältst damit alle Punkte $(x|y|z)$ mit $z=x-y$ oder $x-y-z=0$. Dies führt zu der dargestellten Ebene:

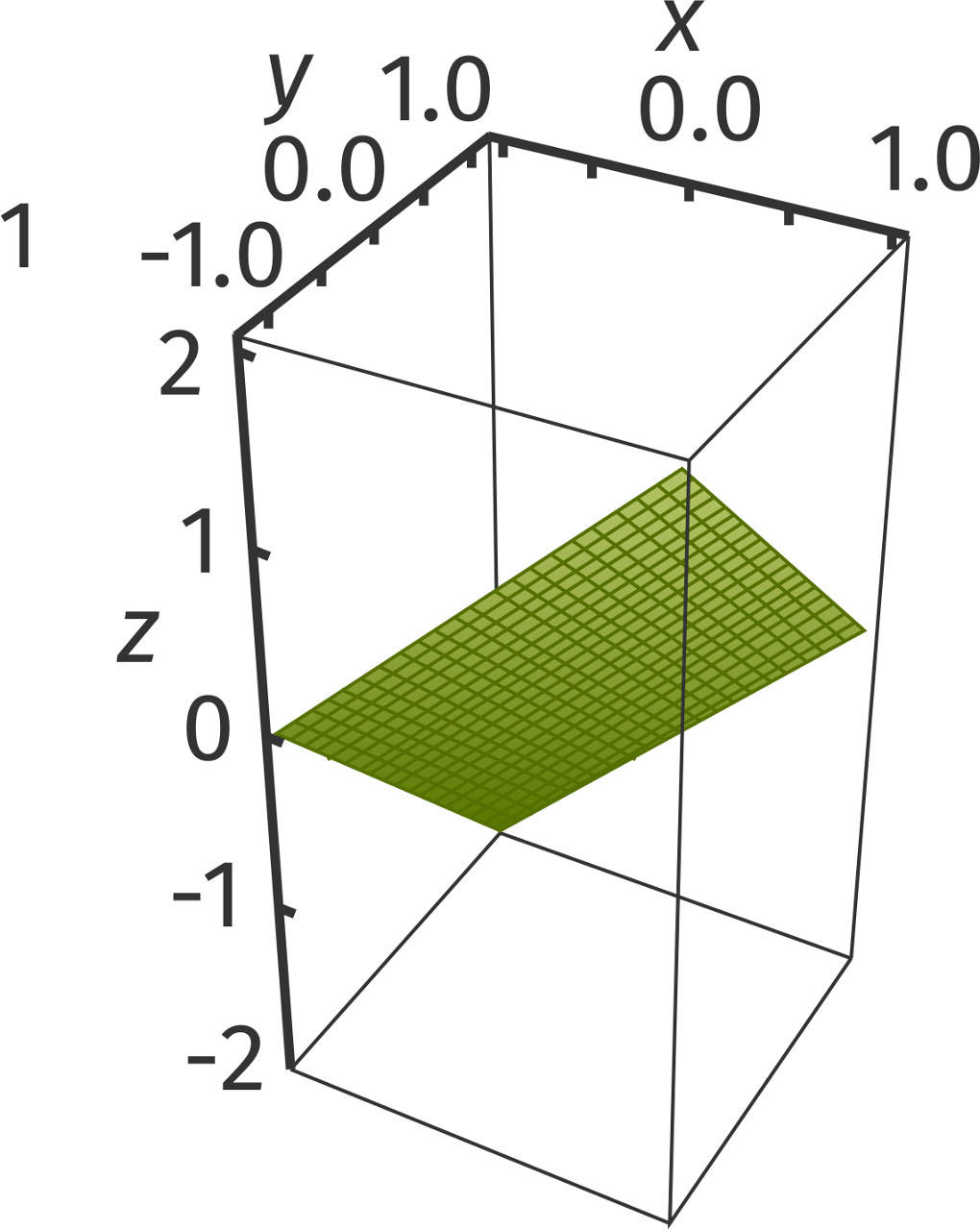
Paraboloid

Die Funktion $f$ mit $f(x,y)=x^{2}+y^{2}$ führt zu einem Paraboloid.

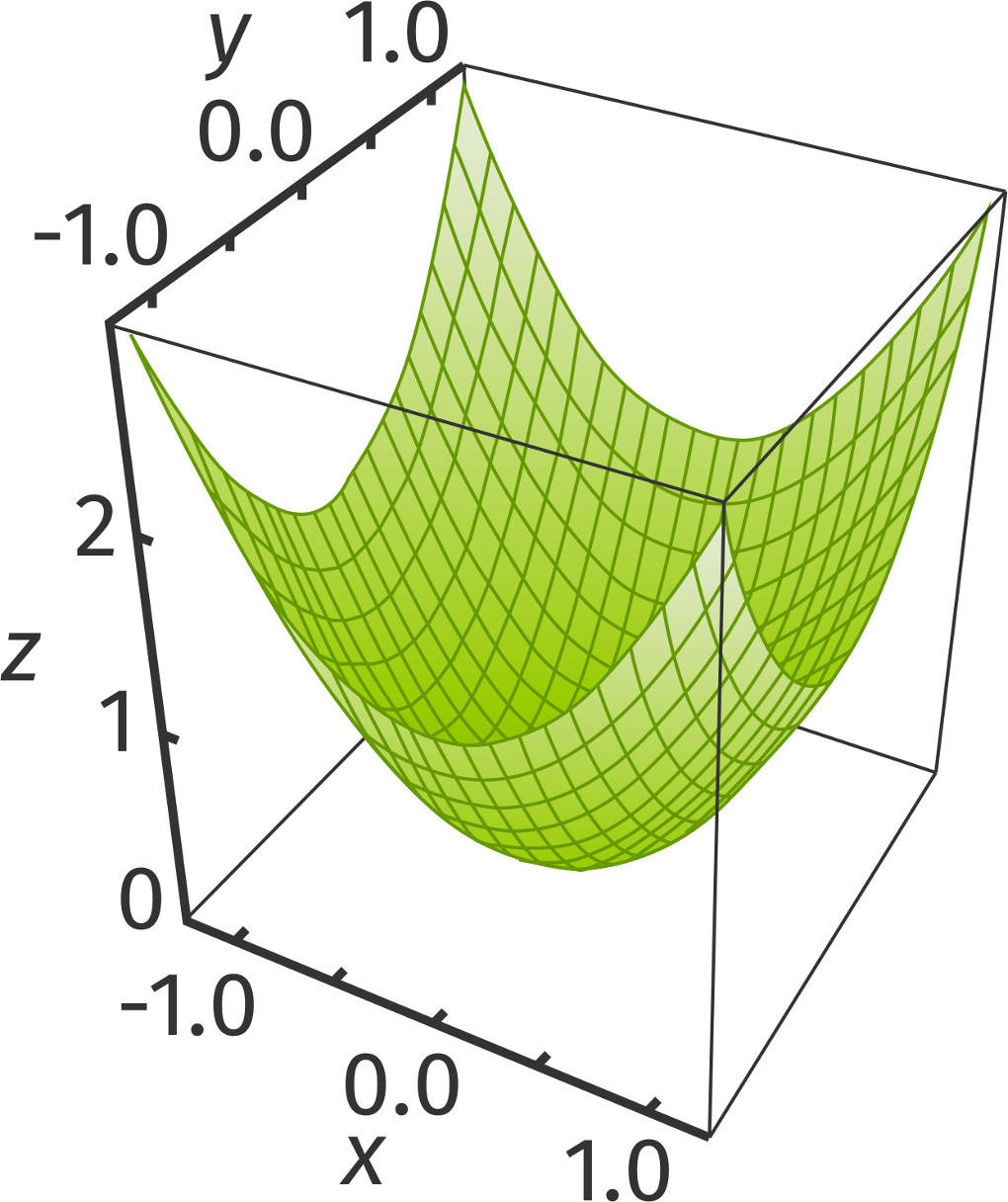
Hyperbolisches Paraboloid

Zuletzt kommen wir zu der Funktion $f$ mit $f(x;y)=x^{2}-y^{2}$ mit einem hyperbolischen Paraboloid als Funktionsgraphen.

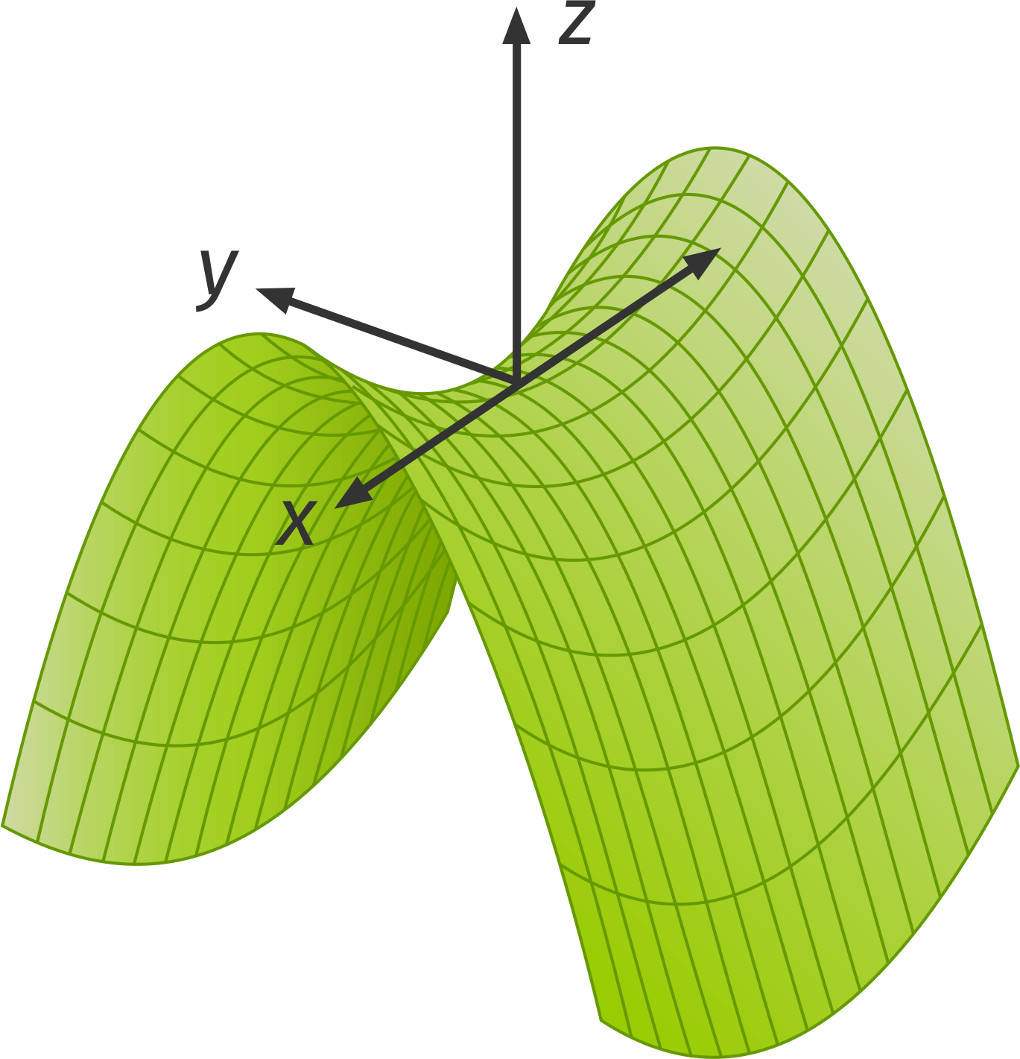
Bei allen dargestellten Flächen im Raum kann es schwierig sein, diese genau zu erkennen. Deshalb werden Schnitte dieser Flächen parallel zu den Koordinatenebenen durchgeführt. Diese lernst du nun kennen.

Höhenlinien

Die Höhenlinien entsprechen Schnitten durch die Fläche im Raum parallel entweder zu der $x$-$z$- oder der $y$-$z$-Koordinatenebene. Das bedeutet, dass entweder $y$ oder $x$ konstant gehalten werden.

Für $y=0$ erhältst du im Falle des Paraboloids zu $f(x;y)=x^{2}+y^{2}$ die Funktion $z=x^{2}$, deren Funktionsgraph eine Parabel in der $x$-$z$-Ebene ist.

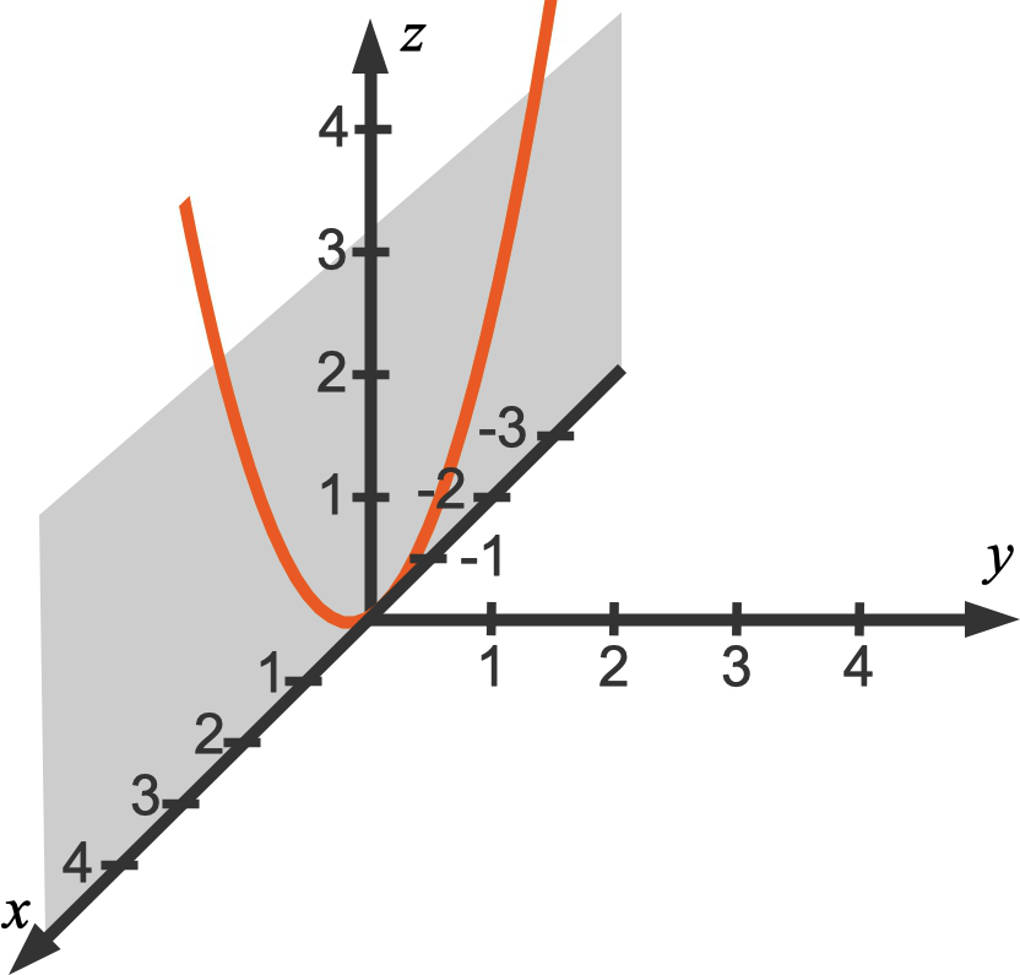
Ebenso erhältst du Parabeln in Ebenen parallel zu der $y$-$z$-Ebene.

Übrigens: Die Höhenlinien des hyperbolischen Paraboloids sind ebenfalls Parabeln. Parallel zur $x$-$z$-Ebene sind diese nach oben geöffnet und parallel zur $x$-$y$-Ebene nach unten geöffnet.

Isoquanten

Du kannst die Fläche im Raum auch parallel zur $x$-$y$-Ebene schneiden. So erhältst du die Isoquanten. Dies sind die Höhenlinien bei konstantem $z$. Du kannst dir dies so vorstellen: Du schaust von oben auf die Fläche im Raum.

Wir schauen uns noch einmal die Funktion $f$ mit zwei Veränderlichen an:

$f(x;y)=x^{2}+y^{2}$

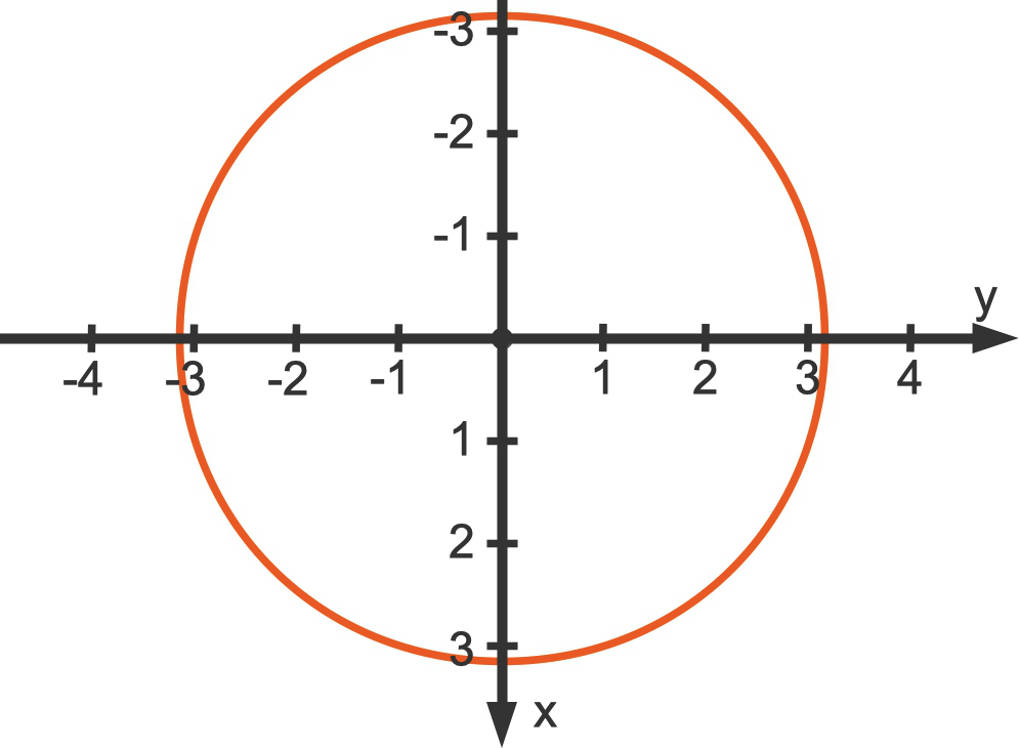
Sei nun $z=z_{0}$ konstant, so erhältst du $x^{2}+y^{2}=z_{0}$. Der zugehörige Funktionsgraph ist ein Kreis parallel zur $x$-$y$- Ebene mit einem Mittelpunkt auf der $z$-Achse.