Potenzfunktionen mit ganzzahligen Exponenten

Inhaltsverzeichnis zum Thema

• Was ist eine Potenzfunktion?
• Aufteilung der Potenzfunktionen
• Spezialfall $z=0$
• Beispiel

Was ist eine Potenzfunktion?

Unter einer Potenzfunktion versteht man in der Regel eine Funktion der Form $f(x)=x^{z}$ wobei $x\in \mathbb{R}$ und $z\in\mathbb{Z}$ gilt.

Zu den Potenzfunktionen zählen ein paar Funktionen, die du vielleicht bereits kennst. Die lineare Funktion $f(x)=x$, die Normalparabel $f(x)=x^{2}$ oder auch die Hyperbel $f(x)=x^{-1}$ gehören dazu. Weil der Exponent $z$ eine beliebige ganze Zahl sein kann, gibt es aber unendlich viele Funktionen dieser Art!

Aufteilung der Potenzfunktionen

Damit du den Überblick trotzdem nicht verlierst, siehst du im Folgenden, wie man diese in sinnvolle Gruppen unterteilen kann. Teile die Potenzfunktionen nach ihren Exponenten auf. Unterscheide dabei zunächst zwischen geraden und ungeraden, dann nochmals zwischen positiven und negativen Exponenten. So erhältst du vier Gruppen mit Potenzfunktionen ähnlicher Eigenschaften:

Sieh dir nun die Funktionsgraphen der vier Gruppen an. An diesen kannst du die Eigenschaften und Gemeinsamkeiten gut erkennen:

Spezialfall $z=0$

Aber halt! Ist dir aufgefallen, dass die Funktion $f(x)=x^{0}$ fehlt? Die Zahl $0$ ist ja weder gerade, ungerade, positiv oder negativ. Deshalb ist diese Funktion auch ein Spezialfall. Denn für alle $x\in\mathbb{R}\setminus \lbrace 0 \rbrace $ gilt: $x^{0} =1$.

Aber wieso ist die Null ausgeschlossen? Der Ausdruck $0^{0}$ ist in der Mathematik nicht definiert. Es gibt also keine sinnvolle, allgemeine Festlegung. Deshalb hat dieser konstante Graph ein unendlich kleines „Loch“ bei $x=0$.

Beispiel

Sehen wir uns die Funktion $f(x)=x^{-3}$ einmal näher an. Der Exponent ist ungerade und negativ. Der Definitionsbereich, also alle Zahlen, die man für $x$ einsetzen darf, sind alle reellen Zahlen ohne Null: $\mathbb{D}=\mathbb{R}\setminus \lbrace 0 \rbrace$. Wir erinnern uns:

$x^{-3} = \dfrac{1}{x^{3}}$

Unsere Funktion ist also ein Bruch! Für $x=0$ müssten wir durch $0$ teilen, was nicht erlaubt ist.

Die Wertemenge, also alle $y$-Werte, die wir mit dieser Funktion erhalten können, sind auch alle reellen Zahlen ohne Null: $\mathbb{W}=\mathbb{R}\setminus \lbrace 0 \rbrace $. Aber warum ist die Null ausgeschlossen? Ganz einfach: Ein Bruch kann nur dann den Wert $0$ annehmen, wenn sein Zähler $0$ ist. Unsere Funktion hat im Zähler immer die Zahl $1$, egal was wir für $x$ einsetzen!

Für die Nullstellen setzen wir immer $f(x):=0$. Wir suchen also alle $x$-Werte, für die der $y$-Wert $0$ ist. Wie wir vorhin gesehen haben, ist das allerdings ein Ding der Unmöglichkeit. Daher hat unsere Funktion keine Nullstellen.

Die Funktion ist punktsymmetrisch zum Ursprung $P(0/0)$, weil der Exponent ungerade ist. Warum das so ist, wirst du gleich sehen. Stell dir die Punktsymmetrie einfach als zweimalige Achsenspiegelung vor: Ein Punkt im ersten Quadranten (rechts oben im Koordinatensystem) wird über die $x$-Achse erst nach unten, dann über die $y$-Achse nach links gespiegelt.

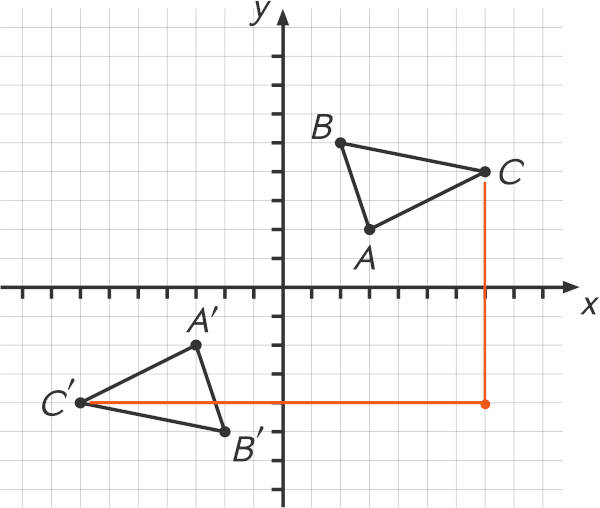
Rechnerisch gilt dann für alle $x\in\mathbb{D}:f(x)=-f(-x)$. In unserem Beispiel muss also gelten:

$\dfrac{1}{x^{3}}=-\left(\dfrac{1}{\left(-x\right)^{3}}\right)$

$(-x)^{n}$ ist immer negativ, wenn $n$ ungerade, also z.B. $3$ ist. Vor der Funktion, also dem Bruch steht nochmal ein Minuszeichen. Diese zwei Minuszeichen ergeben gemeinsam wieder Pluszeichen. Somit ist die Gleichung erfüllt. Wir konnten rechnerisch zeigen, dass $f$ punktsymmetrisch zum Ursprung ist.

Das Beispiel $f(x)=x^{-1}$ wird in folgendem Video ausführlich behandelt: