Grundlagen zu linearen Funktionen
Was ist eine lineare Funktion? Hier lernst du die wichtigsten Grundlagen zu linearen Funktionen kennen: Wie eine lineare Funktion aufgebaut ist, wie der Graph einer linearen Funktion aussieht und wie man eine lineare Funktionsgleichung aufstellt.
Beliebteste Videos
Jetzt mit Spaß die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine lineare Funktion?
- Der Graph einer linearen Funktion
- Bedeutung der Parameter
- Aufstellen einer linearen Funktionsgleichung
Was ist eine lineare Funktion?
Wie du vielleicht weißt, geben Funktionen zu einem Wert, den du in die Funktion „hineinsteckst“, genau einen Wert heraus. Daher heißen sie auch Zuordnungen: Einem Wert wird (genau) ein anderer zugeordnet.
Die lineare Funktion ist eine Funktion, deren Funktionsgraph eine Linie ist. Etwas mathematischer ausgedrückt, heißen diese Linien Geraden. Eine lineare Funktionsgleichung sieht allgemein so aus:
$f(x)=m\cdot x+b$.
Anstelle von $f(x)$ können wir auch $y$ schreiben:
$y=m\cdot x+b$.
Wir wollen einmal näher untersuchen, was die Buchstaben bedeuten:
- Die Variable $y$ ist abhängig von der Variablen $x$ und heißt Funktionswert. Anstelle von $y$ können wir auch $f(x)$ schreiben – wir sagen „f von x“.
- $m$ ist der Faktor (auch Koeffizient) vor $x$ und beschreibt die Steigung der Geraden.
- $x$ ist die unabhängige Variable und wird auch als Argument der Funktion bezeichnet.
- $b$ wird als Konstante bezeichnet. Weil sie die Schnittstelle mit der $y$-Achse beschreibt, wird sie auch $y$-Achsenabschnitt genannt.
Der Graph einer linearen Funktion
Mithilfe einer Wertetabelle können wir zu einigen x-Werten die zugehörigen y-Werte bestimmen, indem wir einen Wert $x$ einsetzen und so $y$ berechnen. Schauen wir uns ein Beispiel für eine lineare Funktion an:
$y=2x-3$.
In diesem Beispiel ist die Steigung $m=2$ und $b=-3$ der y-Achsenabschnitt. Hier siehst du eine zu dieser Funktion gehörende Wertetabelle.
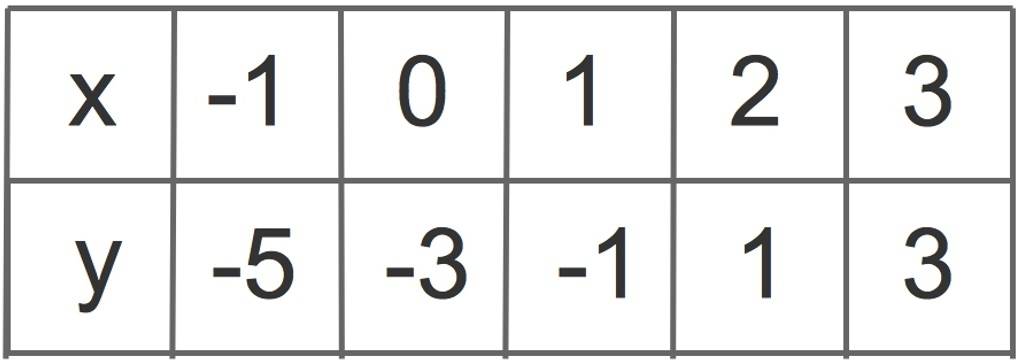
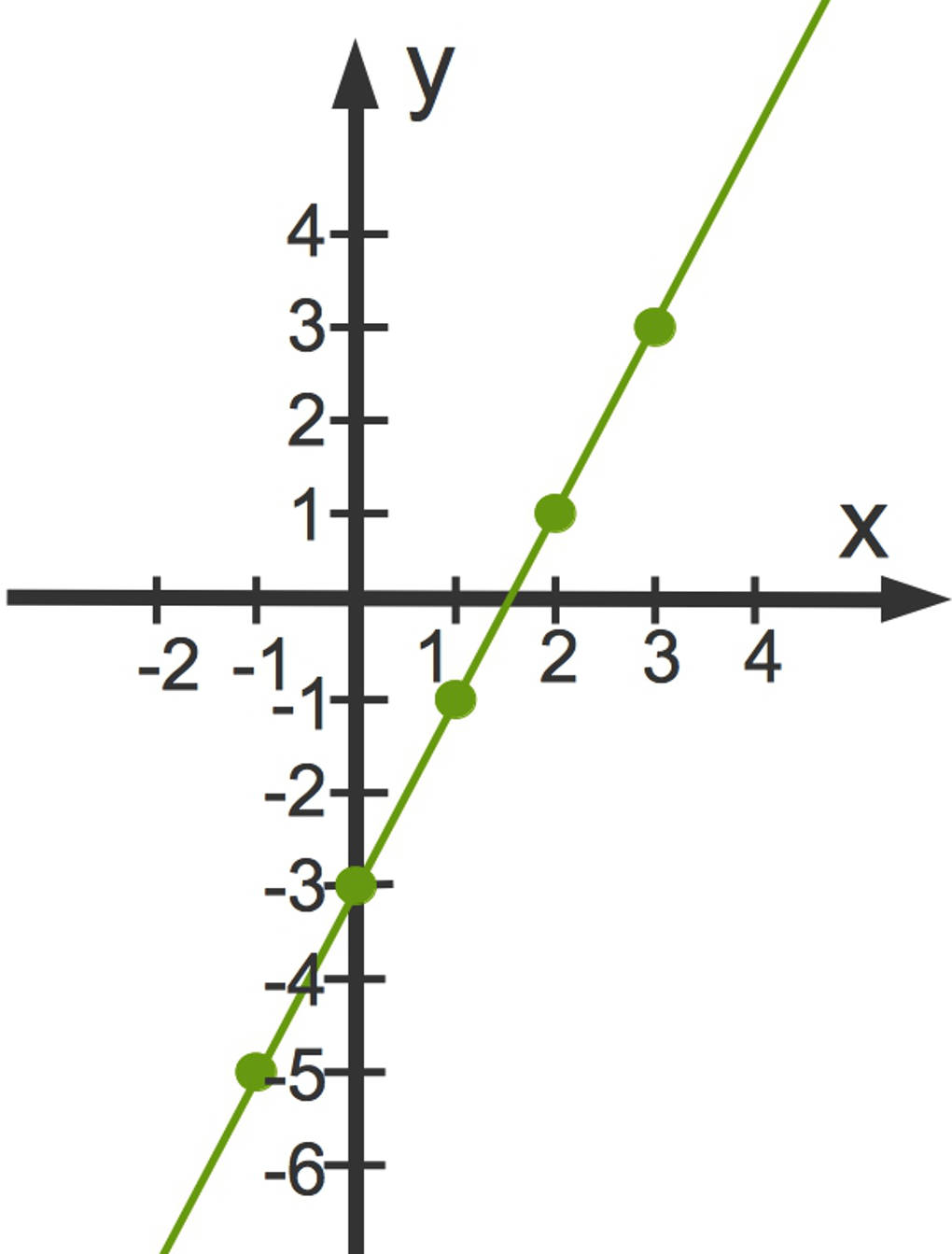
Jetzt können wir die Zahlenpaare $(x|y)$ in ein Koordinatensystem einzeichnen. Diese Punkte verbinden wir miteinander. So erhältst du den Funktionsgraphen dieser linearen Funktion, eine Gerade.
Bedeutung der Parameter
Die Parameter $m$ und $b$ sind für eine Funktion sehr wichtig. Wir können nämlich allein mithilfe von $m$ und $b$ und ohne Wertetabelle den Funktionsgraph zeichnen. Dies wollen wir einmal anhand dieser Funktionsgleichung zeigen:
$f(x)=\frac23x-2$.
Zuerst zeichnen wir den y-Achsenabschnitt. Dieser zeigt an, wo die Gerade die y-Achse schneidet. Ist $b$ eine positive Zahl, so ist der Schnittpunkt oberhalb der x-Achse. Ist $b$ negativ, so ist der Schnittpunkt unterhalb der x-Achse. In unserer Funktionsgleichung ist $b=-2$. Die y-Achse wird also bei $y=-2$ geschnitten.
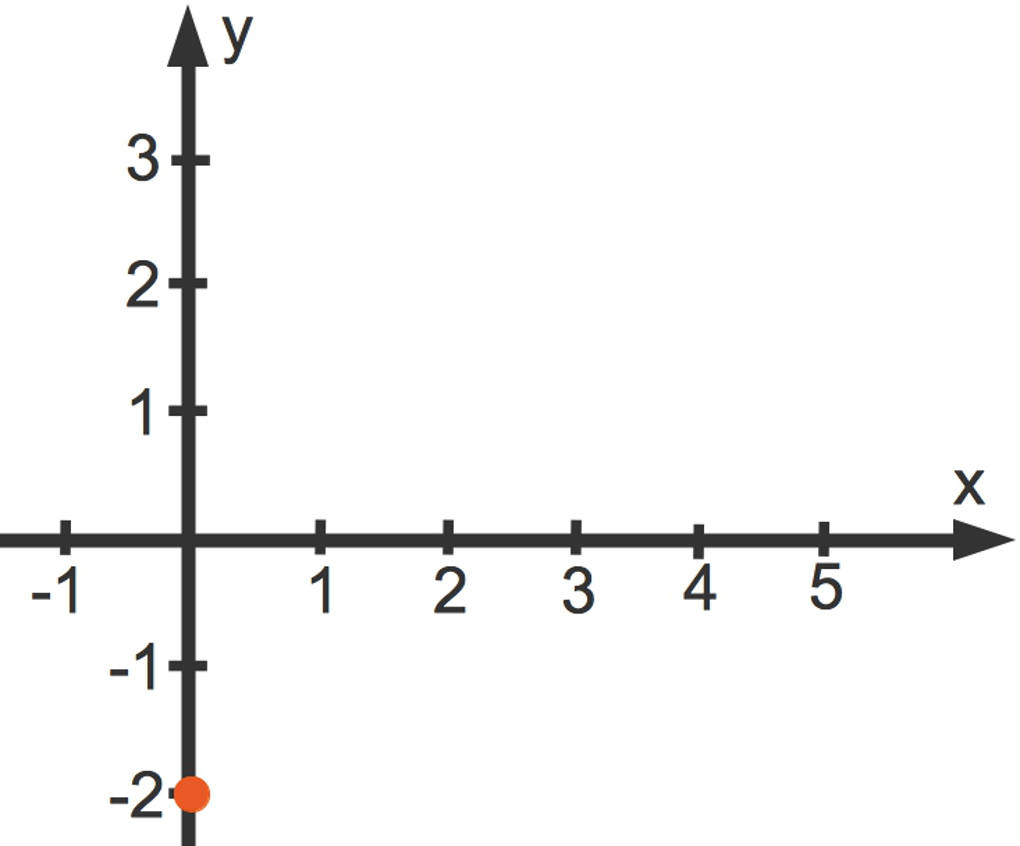
Die Steigung unserer Funktion ist $m=\frac23$. Wie können wir diese in das Koordinatensystem einzeichnen? Wir gehen $3$ Einheiten nach rechts ...
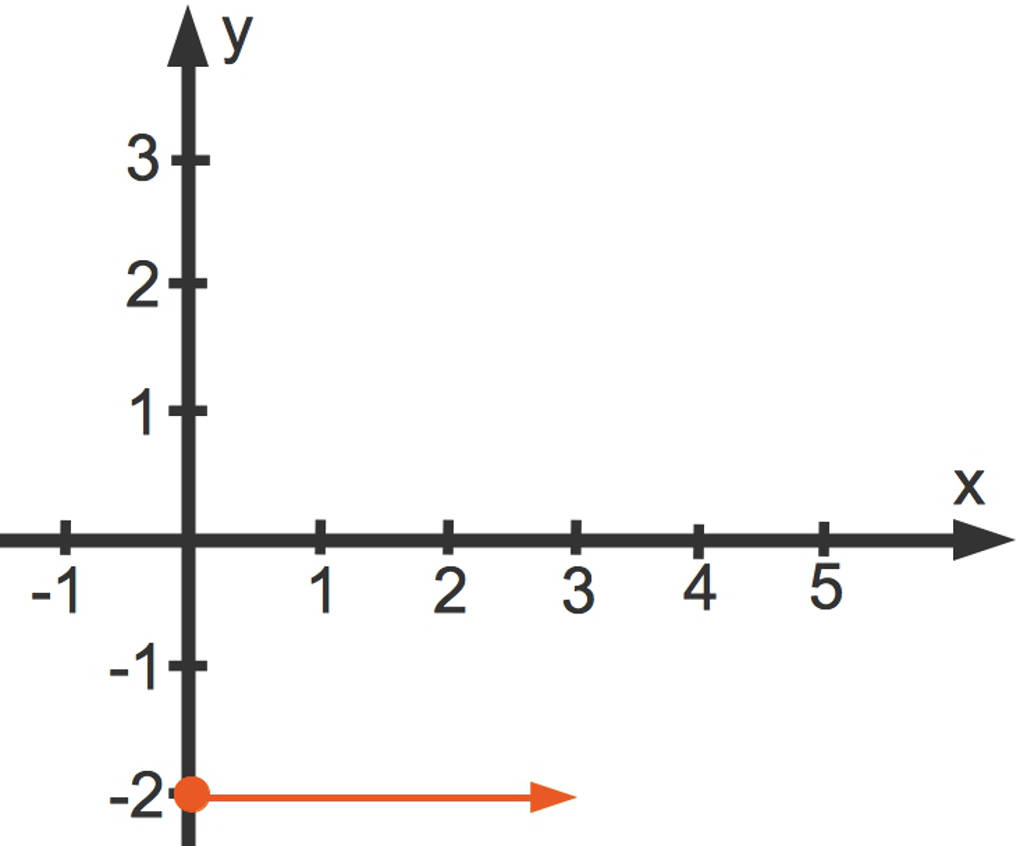
... und von dort $2$ Einheiten nach oben. (Wäre $m$ negativ, würdest du nach unten gehen.) So erhältst du einen weiteren Punkt der Geraden.
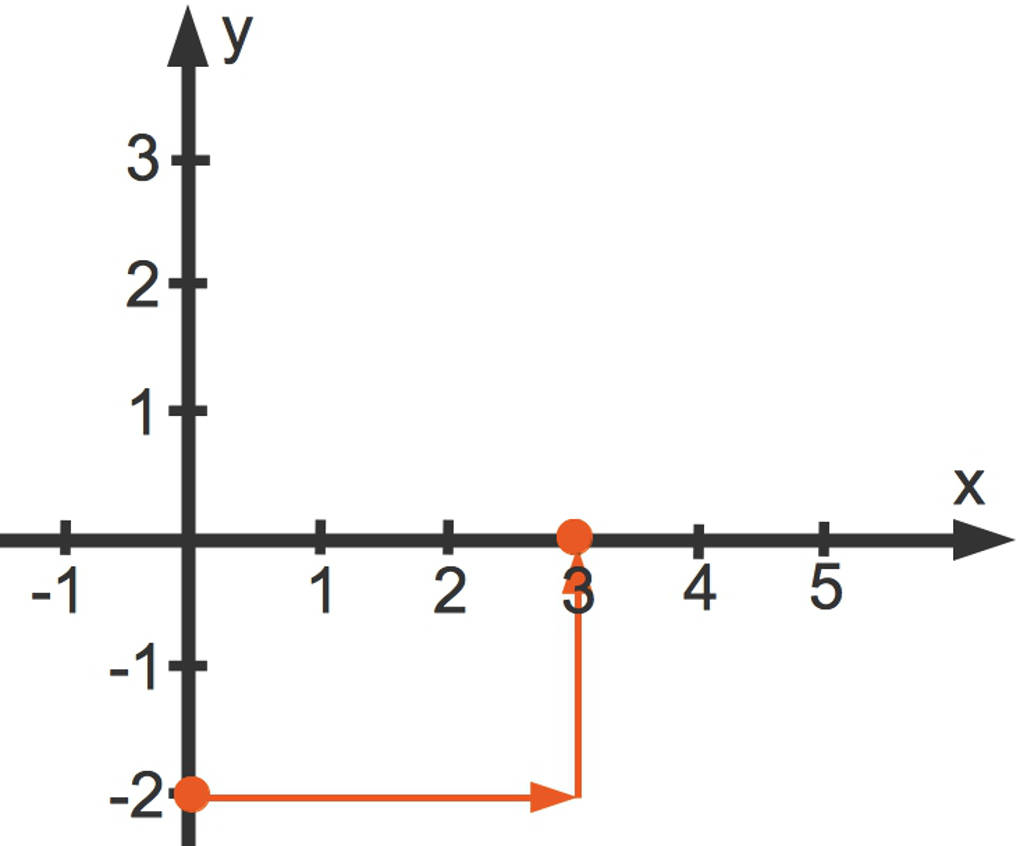
Wir verbinden die beiden Punkte miteinander und erhalten so unsere Gerade.
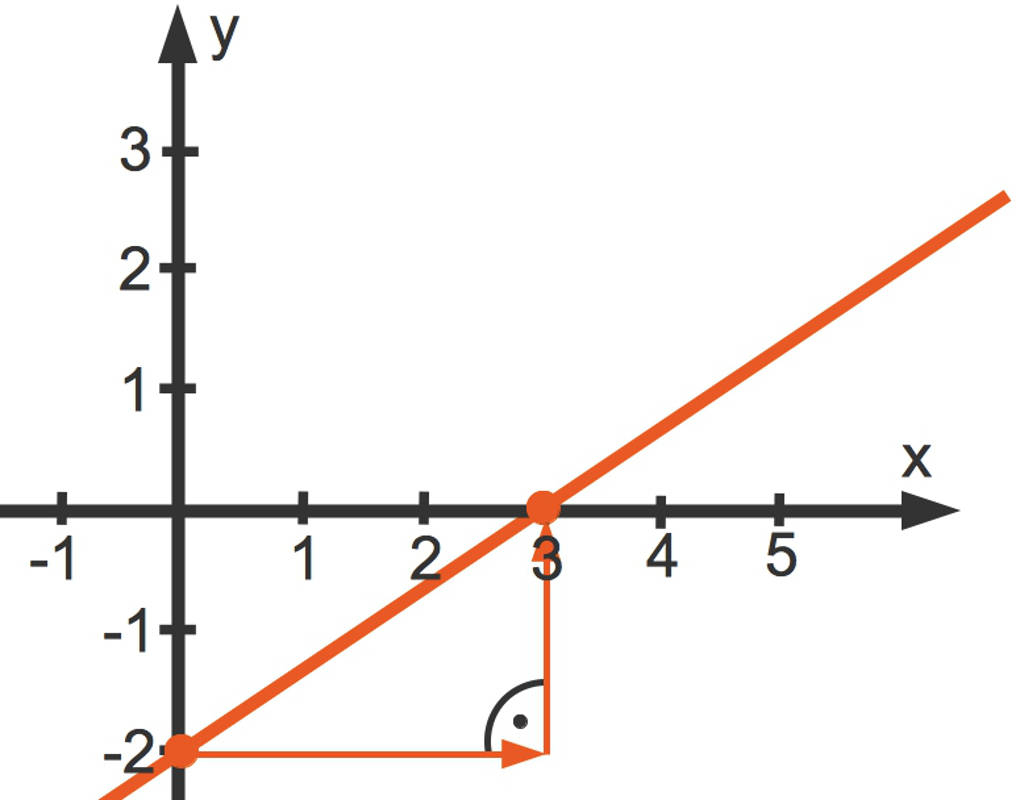
Das rechtwinklige Dreieck, welches du hier erkennen kannst, wird als Steigungsdreieck bezeichnet. Du kannst mithilfe des Steigungsdreiecks die Steigung bestimmen.
Die Steigung einer linearen Funktion kann auch als Bruch dargestellt werden. Dann ist der Nenner die Länge der waagerechten Kathete des Dreiecks und der Zähler die Länge der senkrechten Kathete.
Wenn $m>0$ ist, dann steigt die Gerade. Wenn $m<0$ ist, dann fällt die Gerade. Umso größer der Betrag von $m$ ist, desto stärker steigt (oder fällt) die Gerade.
Aufstellen einer linearen Funktionsgleichung
Wir können andersherum die Funktionsgleichung bestimmen, wenn eine Gerade durch zwei Punkte gegeben ist. Schauen wir uns ein Beispiel an.
Durch zwei Punkte $P(3|3)$ und $Q(5|1)$ verläuft eine Gerade. Wie lautet wohl die Geradengleichung?
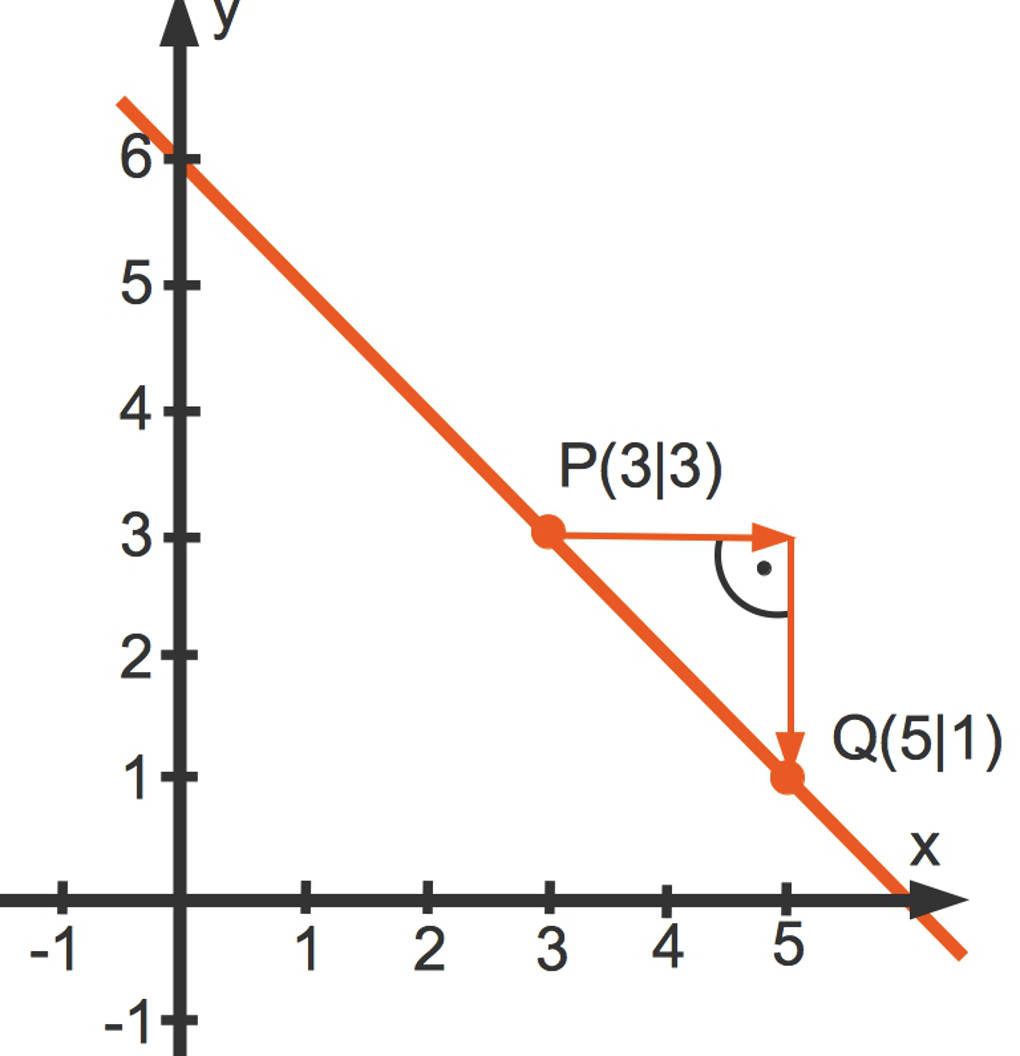
Auch hier können wir ein Steigungsdreieck einzeichnen. Die Steigung lässt sich durch den Quotienten aus senkrechter und waagerechter Kathete berechnen. Das Vorzeichen der Steigung ist negativ, wenn die Gerade fällt.
Die Steigung kannst du mit der Steigungsformel berechnen:
$m=\frac{1-3}{5-3}=-\frac22=-1$.
Allgemein lautet diese Formel für zwei Punkte $P(p_1|p_2)$ und $Q(q_1|q_2)$
$m=\frac{q_2-p_2}{q_1-p_1}$.
Achte darauf, dass die Reihenfolge in Zähler und Nenner gleich ist. Wenn du im Zähler die y-Koordinate von $P$ von der y-Koordinate von $Q$ abziehst, musst du dies in derselben Reihenfolge im Nenner für die x-Koordinaten machen.
Wenn die Steigung schon berechnet wurde, kann nun der y-Achsenabschnitt ermittelt werden. Dafür setzt du die Koordinaten eines der beiden Punkte sowie die berechnete Steigung in die allgemeine Funktionsgleichung $f(x)=mx+b$ ein.
Für den Punkt $Q(5|1)$ erhalten wir dann $1=-1\cdot 5+b$. Diese Gleichung können wir nach $b$ auflösen. Wir erhalten $b=6$ und somit die lineare Funktionsgleichung
$f(x)=-x+6$.
Alle Videos zum Thema
Videos zum Thema
Grundlagen zu linearen Funktionen (8 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Grundlagen zu linearen Funktionen (8 Arbeitsblätter)
-
 Lineare Funktionen – Definition
PDF anzeigen
Lineare Funktionen – Definition
PDF anzeigen -
 Lineare Funktion – Wertetabelle
PDF anzeigen
Lineare Funktion – Wertetabelle
PDF anzeigen -
 Lineare Funktionen zeichnen
PDF anzeigen
Lineare Funktionen zeichnen
PDF anzeigen -
 Schnittpunkte linearer Funktionen
PDF anzeigen
Schnittpunkte linearer Funktionen
PDF anzeigen -
 Steigung von Geraden – y=mx+b
PDF anzeigen
Steigung von Geraden – y=mx+b
PDF anzeigen -
 Geradengleichungen – Normalform (y=mx+b)
PDF anzeigen
Geradengleichungen – Normalform (y=mx+b)
PDF anzeigen -
 Lineare Funktionen – Nullstellen berechnen
PDF anzeigen
Lineare Funktionen – Nullstellen berechnen
PDF anzeigen -
 Lineare Funktionsgraphen – Punktprobe
PDF anzeigen
Lineare Funktionsgraphen – Punktprobe
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Primzahlen
- Geometrische Lagebeziehungen
- Rechteck
- Pq-Formel
- Binomische Formeln
- Trapez
- Volumen Zylinder
- Umfang Kreis
- Quadrat
- Division
- Raute
- Parallelogramm
- Polynomdivision
- Was Ist Eine Viertelstunde
- Prisma
- Mitternachtsformel
- Grundrechenarten Begriffe
- Dreiecksarten
- Quader
- Satz Des Pythagoras
- Dreieck Grundschule
- Erste Binomische Formel
- Kreis
- Standardabweichung
- Flächeninhalt
- Volumen Kugel
- Zahlen In Worten Schreiben
- Meter
- Orthogonalität
- Schriftlich Multiplizieren
- Brüche Multiplizieren
- Potenzgesetze
- Distributivgesetz
- Flächeninhalt Dreieck
- Rationale Zahlen
- Volumen Berechnen
- Brüche Addieren
- Kongruenz
- Exponentialfunktion
- Scheitelpunktform
- Logarithmus
- Erwartungswert
- Skalarprodukt
- Primfaktorzerlegung
- Quadratische Ergänzung
- Zinseszins
- Geradengleichung Aus Zwei Punkten Bestimmen
- Sinusfunktion






















