Kraftwandler als Werkzeuge
Kennzeichen und Arten von Kraftwandlern; Hebel; Sachaufgaben zum Hebel; Wellrad; Seilmaschinen; Der Flaschenzug; Schiefe Ebene; Sachaufgaben zur schiefen Ebene
Inhaltsverzeichnis zum Thema
- Einsatzgebiete von Kraftwandlern
- Der Hebel als Kraftwandler
- Von der Rolle zum Flaschenzug
- Schiefe Ebene
Einsatzgebiete von Kraftwandlern
Schon die Steinzeitmenschen verwendeten Äste und Steine und konnten damit eine größere Kraft ausüben. So entstanden die ersten Werkzeuge und Waffen.
Überall, wo Menschen mit sehr wenig Krafteinsatz viel bewirken wollen, werden Kraftwandler als Werkzeuge eingesetzt. Dies können die Rohrzange, der Wagenheber, der Kran oder auch nur der Kochlöffel in einem Topf sein. Es gibt aber auch Feinwerkzeuge, bei denen die menschliche Kraft reduziert werden muss, um das Werkstück nicht zu beschädigen. Die Pinzette ist solch ein Werkzeug.
Der Hebel als Kraftwandler
Seit der frühe Mensch einen Ast ergriff und mit diesem einen Stein bewegte, setzte er den Hebel als Kraftwandler ein. Der Ast diente als Verlängerung seines eigenen Arms. Durch diese Verlängerung konnte er mit demselben Krafteinsatz mehr Wirkung erzielen.
Nach dieser einfachen Armverlängerung sind auch Bestandteile des Hebels benannt, die für seine Wirkungsweise unentbehrlich sind. Jeder Hebel besitzt einen Drehpunkt (zum Beispiel die Schraube in der Schere). Nur an dieser Stelle verändert der Hebel im Einsatz seine Position nicht.
Auch besitzt der Hebel einen Lastarm.Dieser beschreibt eine Länge vom Drehpunkt bis zum Schwerpunkt der Last. Und drittens besitzt der Hebel einen Hebearm. Dieser beschreibt die Länge vom Drehpunkt bis zum Angriffspunkt der Kraft, zum Beispiel die Stelle, an der wir einen Ast anfassen. Bei der Wippe würde dies so aussehen:

Das Hebelgesetz beschreibt den Zustand, in dem ein Hebel sich im Gleichgewicht befindet.
$\vec{F}_1 \cdot l_1 = \vec{F}_2 \cdot l_2~,~ \frac{\vec{F}_1}{\vec{F}_2}= \frac{l_2}{l_1}$
Von der Rolle zum Flaschenzug
Mit einem einfachen Seil und Rollen (allg. Umlenkpunkten) lassen sich eine Vielzahl von Kraftwandlern konstruieren. Durch diese kann man sowohl die Richtung einer Kraft verändern als auch den notwendigen Betrag der Zugkraft.
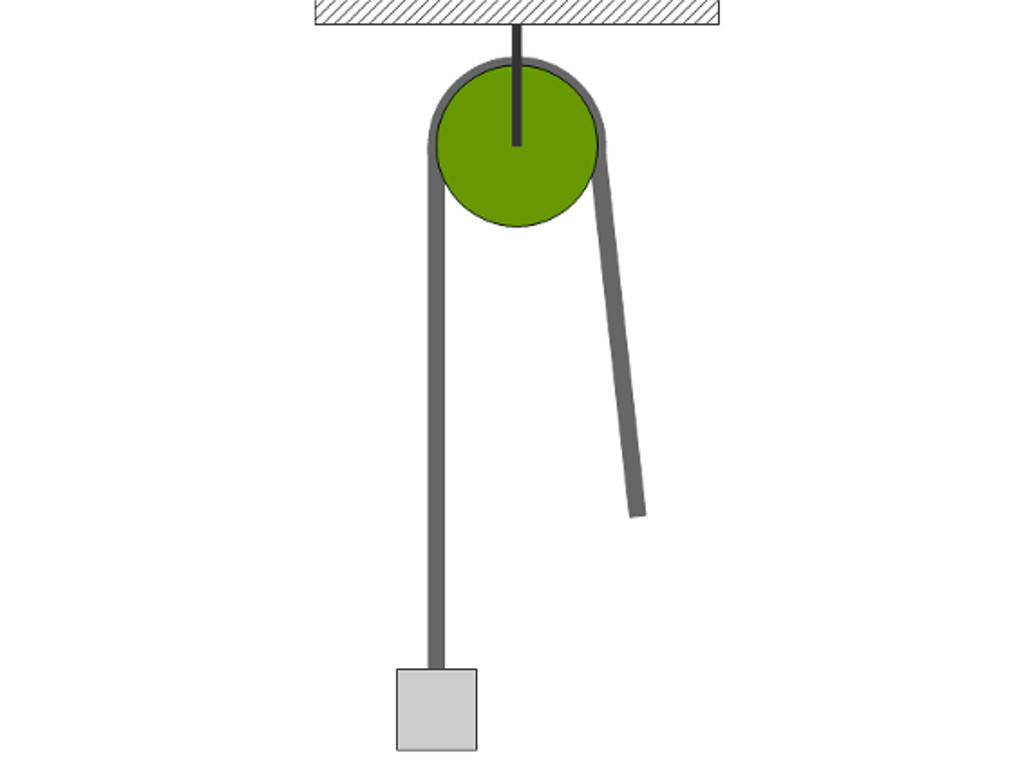
Der einfachste Fall ist die einzelne Umlenkrolle oder auch feste Rolle. Dies ist eine einfache, fest montierte Rolle, über die ein Seil geführt wird. Durch diese Konstruktion wird die Wirkungsrichtung der Zugkraft verändert, der Kraftbetrag verändert sich aber nicht. Auch ist der Zugweg genauso lang wie der Hubweg.
$F_{Zug} = F_{Hub}~,~s_{Zug}=s_{Hub}$
Der Vorteil dieser Konstruktion ist auch gleichzeitig ihr Nachteil. Ist die Rolle an der Decke befestigt, kann man sein Körpergewicht einsetzen, um eine Last nach oben zu ziehen. Gleichzeitig kann man aber auch nur eine Last nach oben bewegen, die kleiner als das eigene Körpergewicht ist.
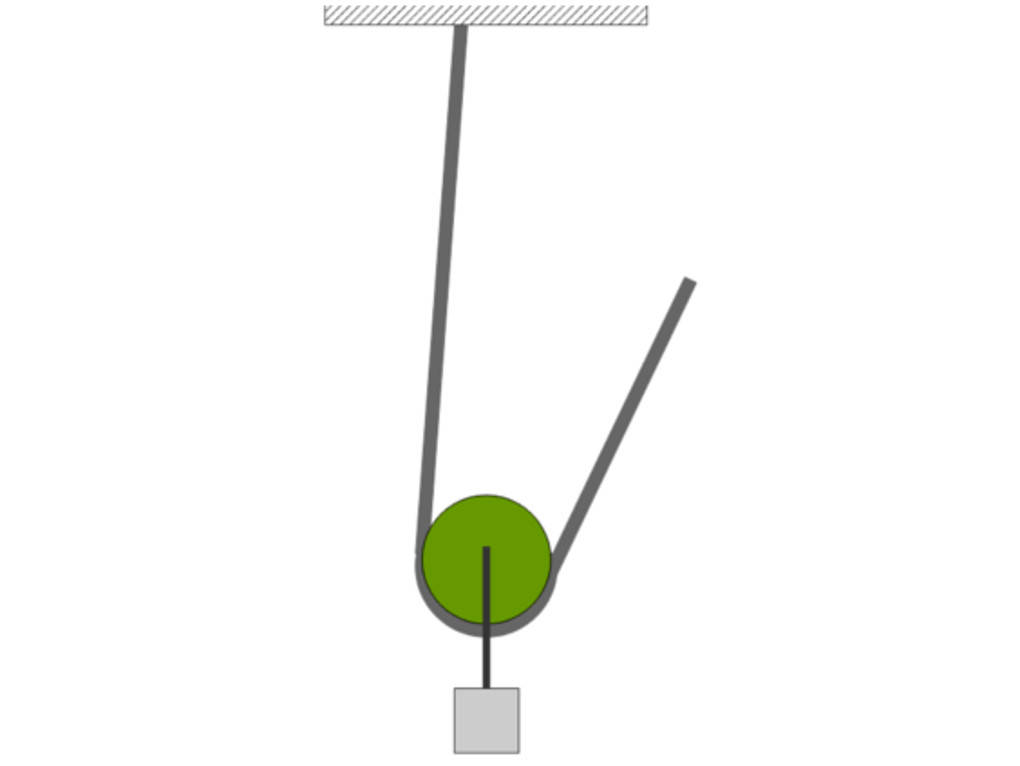
Die zweite Möglichkeit ist die lose Rolle. Bei dieser wird die Rolle an der Last befestigt und ein Seil über diese geführt, welches an einem Ende fest montiert ist. Bei diesem Aufbau verändert sich die die Richtung der Kraft nicht, jedoch wird der Betrag der benötigten Zugkraft halbiert, da sich das Gewicht der Last auf zwei Seilstücke verteilt und wir nur an einem davon ziehen. Dafür ist aber auch der Zugweg doppelt so lang wie der Hubweg.
Damit gleicht sich die Kraftersparnis und die Wegverlängerung wieder aus. Das muss auch nach der goldenen Regel der Mechanik so sein, da die notwendige Arbeit sich nicht verändern darf.
$F_{Zug} = \frac{F_{Hub}}{2}~,~s_{Zug}=2 \cdot s_{Hub}~,~ W_{Zug}=W_{Hub}$
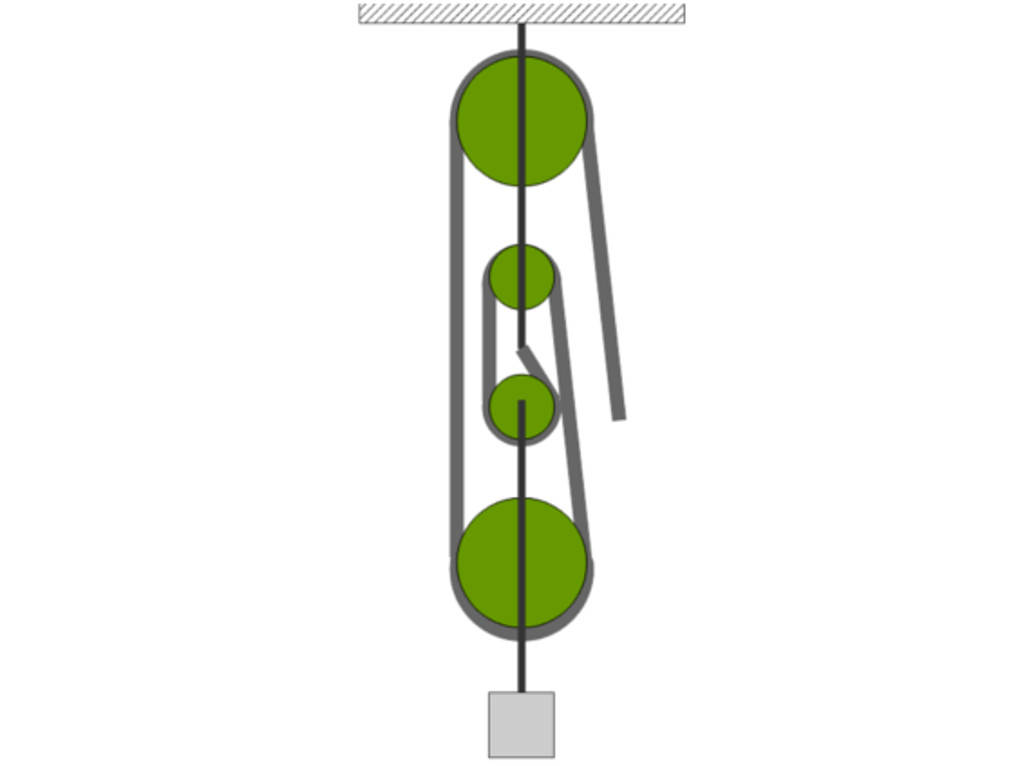
Kombiniert man mehrere lose und feste Rollen, so konstruiert man einen Flaschenzug. Bei diesem wird das Zugseil über mindestens drei Rollen geführt. Das Gewicht der Last verteilt sich nun auf alle tragenden Seile. Damit kann der Betrag der benötigten Zugkraft stark reduziert werden. Mit der Anzahl der tragenden Seile $n$ gilt:
$F_{Zug} = \frac{F_{Hub}}{n}~,~s_{Zug}=n \cdot s_{Hub}~,~ P_{Zug}=P_{Hub}$
Schiefe Ebene
Auch eine einfache Rampe kann die benötigte Kraft zum Heben einer Last reduzieren. Der Physiker bezeichnet dies als schiefe Ebene. Wenn man etwas senkrecht nach oben zieht, würde man die Last in einem 90°-Winkel zum Erdboden nach oben bewegen.
Die schiefe Ebene als Kraftwandler ermöglicht es, die Last in einem beliebigen Winkel zwischen 0° und 90° nach oben zu bewegen. Dabei wird umso mehr Kraft eingespart, je flacher die Rampe ist. Dies kennst du auch vom Wandern: Je steiler der Anstieg, desto mehr kommst du ins Schwitzen. Ist der Anstieg dagegen flach, geht es leichter. Du brauchst aber auch länger, um dieselbe Höhe zu erreichen.
Hierbei gleichen sich wieder nach der goldenen Regel der Mechanik die Kraftersparnis und die Wegverlängerung genau aus, sodass die mechanische Arbeit konstant bleibt. Dabei wird jedoch die Reibung auf der Rampe ignoriert.
Zur genauen Darstellung der Kraftzusammenhänge werden mehrere Kräfte benötigt: Die relevanten Kräfte sind die Hangabtriebskraft $\vec{F}H$, der wir entgegen wirken müssen, die Normalkraft $\vec{F}N$, die senkrecht zur schiefen Ebene orientiert ist und die Reibung auf der Ebene bewirkt, und die Gewichtskraft $\vec{F}_G$, die weiterhin zum Erdmittelpunkt wirkt.
Um die Last nach oben zu bewegen, müssen wir eine größere Kraft aufbringen als die Hangabtriebskraft. Zeichnerisch lassen sich die Größen der Kräfte mit dem Kräfteparallelogramm bestimmen.
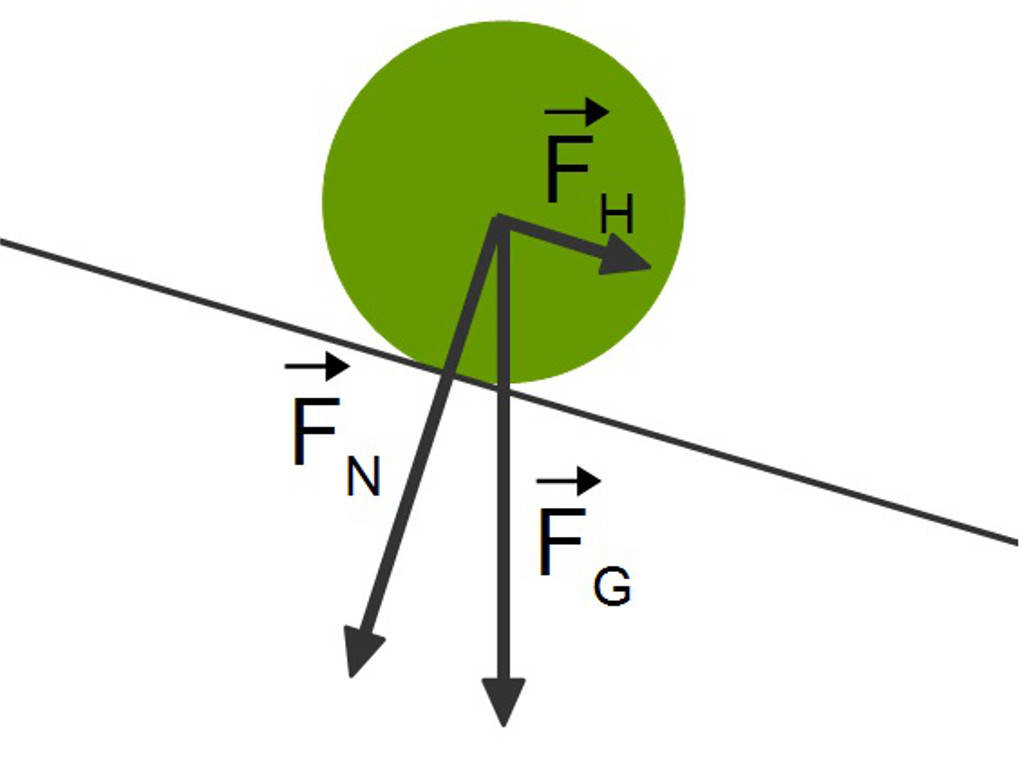
$\frac{F_H}{F_G}=\frac{h}{l}~,~F_H=F_G\cdot sin\alpha~,~F_N=F_G\cdot cos\alpha$
Alle Videos zum Thema
Videos zum Thema
Kraftwandler als Werkzeuge (5 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Kraftwandler als Werkzeuge (5 Arbeitsblätter)
Beliebteste Themen in Physik
- Temperatur
- Schallgeschwindigkeit
- Dichte
- Drehmoment
- Transistor
- Lichtgeschwindigkeit
- Elektrische Schaltungen – Übungen
- Galileo Galilei
- Rollen- Und Flaschenzüge Physik
- Radioaktivität
- Aufgaben zur Durchschnittsgeschwindigkeit
- Lorentzkraft
- Beschleunigung
- Gravitation
- Ebbe und Flut
- Hookesches Gesetz Und Federkraft
- Elektrische Stromstärke
- Elektrischer Strom Wirkung
- Reihenschaltung
- Ohmsches Gesetz
- Freier Fall
- Kernkraftwerk
- Reflexionsgesetz: Ebener Spiegel – Übungen
- Was sind Atome
- Aggregatzustände
- Infrarot, Uv-Strahlung, Infrarot Uv Unterschied
- Isotope, Nuklide, Kernkräfte
- Transformator
- Lichtjahr
- Si-Einheiten
- Fata Morgana
- Gammastrahlung, Alphastrahlung, Betastrahlung
- Kohärenz Physik
- Mechanische Arbeit
- Schall
- Elektrische Leistung
- Dichte Luft
- Ottomotor Aufbau
- Kernfusion
- Trägheitsmoment
- Heliozentrisches Weltbild
- Energieerhaltungssatz Fadenpendel
- Linsen Physik
- Ortsfaktor
- Interferenz
- Diode und Photodiode
- Wärmeströmung (Konvektion)
- Schwarzes Loch
- Frequenz Wellenlänge
- Elektrische Energie







 Der Hebel und das Hebelgesetz
Der Hebel und das Hebelgesetz
 Die schiefe Ebene
Die schiefe Ebene
 Rollen und Flaschenzüge
Rollen und Flaschenzüge
 Drehmoment, Wellrad und Fahrrad
Drehmoment, Wellrad und Fahrrad
 Flaschenzug (Übungsvideo)
Flaschenzug (Übungsvideo)









