Parabelscharen – Beispiele


in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Grundlagen zum Thema Parabelscharen – Beispiele
Dieses Übungsvideo beschäftigt sich mit Aufgaben zum Thema Parabelscharen. Nachdem wir kurz noch einmal wiederholt haben, wie die Parameter a, b und c die Parabel der Form f(x)=ax2+bx+c beeinflussen, rechnen wir drei verschiedene Aufgaben zu dem Thema, um den Umgang mit Parabelscharen zu festigen. Viel Spaß!
Parabelscharen – Beispiele Übung
-
Beschreibe die Bedeutung der Parameter $a$, $b$ sowie $c$.
TippsHier ist eine Parabel zu sehen. Die zugehörige Funktionsgleichung lautet
$f(x)=x^2-6x+11$.
Es ist also $a=1$, $b=-6$ und $c=11$. Alle Parameter sind durch Zahlen ersetzt.
Diese Parabeln haben alle einen Scheitelpunkt, der die gleiche x-Koordinate hat.
Die zugehörigen Funktionsgleichungen unterscheiden sich durch den Parameter $c$.
Jede dieser Parabeln gehört zu einer Funktionsgleichung $f(x)=ax^2$.
Es ist also $b=c=0$.
LösungDie allgemeine Darstellung einer quadratischen Funktion lautet $f(x)=ax^2+bx+c$.
Wenn jeder Parameter durch eine Zahl ersetzt wird, erhält man eine spezielle quadratische Funktion mit der zugehörigen Parabel.
Wenn allerdings mindestens ein Parameter erhalten bleibt, spricht man von einer Parabelschar, da zu jedem Wert für diesen Parameter eine andere Parabel gehört.
Man kann sich nun die folgenden Fälle anschauen.
$a$ und $b$ sind fest und $c$ kann verändert werden:
Die Scheitelpunkte aller Graphen liegen auf einer Geraden parallel zur y-Achse. Der Graph wird mit verändertem $c$ entlang der y-Achse verschoben. Dies ist in dem nebenstehenden Bild zu sehen.
$b$ und $c$ sind fest und $a$ kann verändert werden:
Alle Graphen der Parabelschar haben einen Punkt gemeinsam. Und zwar schneiden alle Graphen die y-Achse an derselben Stelle. Der Graph wird mit verändertem $a$ gestaucht oder gestreckt. Wenn $a$ negativ ist, wird der Graph sogar gespiegelt, ist also nach unten geöffnet.
$a$ und $c$ sind fest und $b$ kann verändert werden:
Alle Scheitelpunkte der Graphen liegen auf einer gemeinsamen Kurve. Diese heißt Ortskurve. Der Graph wird mit verändertem $b$ entlang der x- und entlang der y-Achse verschoben.
-
Stelle die zugehörige Funktionsgleichung $i(x)=ax^2+bx+c$ zu den Punkten $Q_1(-2|1)$ und $Q_2(2|1)$ auf.
TippsWenn ein Punkt $Q(q_x|q_y)$ auf dem Funktionsgraphen zu $f(x)=ax^2+bx+c$ liegt, gilt
$f(q_x)=q_y$, also
$a\cdot q_x^2+b\cdot q_x+c=q_y$.
Zum Beispiel gilt für $Q_1$
$f(-2)=1$.
Die Gleichung, die nach $c$ umgeformt wird, lautet $4a+c=1$.
LösungUm die Parameter eindeutig zu bestimmen, muss man ebenso viele Punkte kennen, wie es Parameter gibt: also drei. Da nur zwei Punkte bekannt sind, wird dies zu einer Parabelschar führen.
Wir setzen zuerst $Q_1(-2|1)$ in die allgemeine quadratische Funktionsgleichung ein. Diese ist hier zu sehen.
$i(-2)=1$, also $\text{I}$ $4a-2b+c=1$.
Dasselbe tun wir dann mit $Q_2(2|1)$:
$i(2)=1$, also $\text{II}$ $4a+2b+c=1$.
Wenn man von der unteren der beiden Gleichungen die obere subtrahiert, erhält man $4b=0$, also $b=0$. Dies setzen wir in die erste Gleichung ein und erhalten
$4a+c=1$.
Diese Gleichung kann nach $c$ umgeformt werden zu $c=1-4a$.
Damit lautet die Funktionsgleichung $i(x)=ax^2+1-4a$.
Es taucht nur noch der Parameter $a$ auf. Dies ist also eine Parabelschar.
-
Entscheide, welche der Parabeln zu welchem Parameter gehört.
TippsFür $a$ gelten unter anderem diese Eigenschaften:
- Wenn die Parabel nach oben geöffnet ist, ist $a$ positiv,
- Wenn die Parabel nach unten geöffnet ist, ist $a$ negativ.
Schaue dir Punkte an, die du gut ablesen kannst und prüfe, ob diese auf dem Funktionsgraphen liegen.
Ist die Parabel breiter (also gestaucht), dann ist entweder $0<a<1$ oder $-1<a<0$.
Ist die Parabel schmaler (also gestreckt), dann ist entweder $a>1$ oder $a<-1$.
LösungAlle diese Parabeln haben den Scheitelpunkt gemeinsam.
Was unterscheidet diese Parabeln?
Die blaue und grüne sind nach oben geöffnet, also ist hier $a>0$. Die beiden anderen Parabeln sind nach unten geöffnet. Das bedeutet, dass $a<0$ sein muss.
Die grüne Parabel gehört zu $a=1$. An dieser kann man sich orientieren:
- Die blaue Parabel ist breiter als die grüne, also ist $0<a<1$. Da die y-Achse bei $1,5=2-0,5$ geschnitten wird, ist $a=0,5$.
- Die rote Parabel hat dieselbe Öffnung wie die grüne, aber ist gespiegelt. Das bedeutet $a=-1$.
- Die orange Parabel ist schmaler als die rote. Das bedeutet, dass $a<-1$ sein muss. Wenn man von der x-Koordinate $1$ des Scheitelpunktes um eine Einheit nach links (oder rechts) geht, muss man zwei Einheiten nach unten gehen. Dies führt zu $a=-2$.
-
Bestimme die jeweilige Funktionsgleichung.
TippsFür $f(x)=ax^2+bx+c$ ist $c$ die Stelle, an welcher die Parabel die y-Achse schneidet.
Die blaue Parabel ist die Normalparabel $a=1$.
- Die grüne Parabel ist weiter, also ist $0<a<1$.
- Die orange Parabel ist enger, also ist $a>1$.
An dem Streckfaktor $a$ kannst du auch erkennen, ob die Parabel nach oben oder nach unten geöffnet ist.
- Ist $a>0$, dann ist die Parabel nach oben geöffnet.
- Ist $a<0$, dann ist die Parabel nach unten geöffnet.
Wenn du den Scheitelpunkt $S(x_s|y_s)$ einer Parabel kennst, kannst du die Funktionsgleichung in Scheitelpunktform angeben:
$f(x)=a(x-x_s)^2+y_s$.
Dabei ist $a$ der Streckfaktor.
LösungWie hängen die Parameter $a$, $b$ oder $c$ mit der Form und Lage einer Parabel zusammen?
Zuerst schauen wir uns den Streckfaktor $a$ an:
Ist $a$ positiv, dann ist die Parabel nach oben geöffnet:
- Für $a>1$ ist die Parabel schmaler (sie steigt schneller) und
- für $0<a<1$ ist sie breiter als die Normalparabel.
- Für $a<-1$ ist die Parabel schmaler und
- für $-1<a<0$ breiter als die Normalparabel.
Den Parameter $b$ kann man am Scheitelpunkt (genauer: dessen x-Koordinate) ablesen.
Sei $f(x)=ax^2+bx+c$ die allgemeine Funktionsgleichung in Parameterform, dann ist die x-Koordinate des Scheitelpunktes gegeben durch
$x_s=-\frac{b}{2a}$.
Durch Einsetzen der x-Koordinate in die Funktionsgleichung erhält man die y-Koordinate des Scheitelpunktes.
Somit gehören die Parabeln zu den folgenden Funktionsgleichungen:
- Die grüne Parabel gehört zu $f(x)=x^2-1$. Hier ist $b=0$, also $x_s=0$.
- Die rote Parabel besitzt den Scheitelpunkt $S(2|0)$ und hat den Streckfaktor $a=1$. Also gehört hierzu die Gleichung $f(x)=(x-2)^2=x^2-4x+4$. Hier ist $b=-4$ und $a=1$, also $x_s=2$.
- Die blaue Parabel ist nach unten geöffnet und hat den y-Achsenschnittpunkt $2$. Der Scheitelpunkt ist $S(0|2)$. Damit lautet die zugehörige Funktionsgleichung $f(x)=ax^2+2$. Da der Punkt $P(1|0)$ auf der Parabel liegt, ist $f(1)=a+2=0$ und somit $a=-2$. Dies führt zu der Funktionsgleichung $f(x)=-2x^2+2$. Hier ist wieder $b=0$ und somit auch $x_s=0$.
- Die Funktionsgleichung zu der orangen Parabel ist gegeben durch $f(x)=-\frac12x^2+2x-1$. Dies kann man zum Beispiel am Scheitelpunkt $S(2|1)$ sowie am y-Achsenabschnitt $-1$ erkennen. Auch hier kann die x-Koordinate des Scheitelpunktes mit Hilfe von $a=-\frac12$ sowie $b=2$ berechnet werden: $x_s=-\frac2{2\cdot \left(-\frac12\right)}=2$.
-
Fasse die Veränderungen des Funktionsgraphen zusammen.
TippsWenn du die blaue Parabel um eine Einheit nach links verschiebst, erhältst du die grüne. Verschiebung um zwei Einheiten nach rechts führt zu der gelben Parabel.
Hier siehst du eine Drehung um $45^\circ$.
Bei einer Funktion gehört zu jedem $x$ maximal ein Funktionswert $y=f(x)$.
LösungDie allgemeine quadratische Funktionsgleichung hat die Form $f(x)=ax^2+bx+c$.
Die Parameter haben verschiedene Bedeutungen, welche man sich zum Beispiel an dem Scheitelpunkt, dem tiefsten oder höchsten Punkt der Parabel klarmachen kann.
Der Streckfaktor $a$:
- Für $a>1$ wird die Parabel gestreckt und für $0<a<1$ gestaucht.
- Ist $a$ negativ, so wird die Parabel gespiegelt.
Mit Hilfe von $b$ kann die x-Koordinate des Scheitelpunktes einer Parabel bestimmt werden. Das bedeutet, dass die Parabel sowohl entlang der x- als auch der y-Achse verschoben wird.
Der Parameter $c$:
Dieser Parameter bewirkt ausschließlich eine Verschiebung entlang der y-Achse. Wenn man in die Funktionsgleichung $x=0$ einsetzt, erhält man $f(0)=c$. An dieser Stelle schneidet die Parabel also die y-Achse.
-
Bestimme den Scheitelpunkt der Funktion, indem du die Anleitung befolgst.
TippsWenn du ausklammerst, musst du jeden Term durch das dividieren, was du ausklammerst. Schau dir dies an einem Beispiel an:
$4x+8=4(4x:4+8:4)=4(x+2)$.
Die Scheitelpunktform einer quadratischen Funktion lautet
$f(x)=a(x-x_s)^2+y_s$.
Der Scheitelpunkt ist dabei $S(x_s|y_s)$.
LösungDie Verschiebung einer Parabel kann man sich gut an dem Scheitelpunkt klarmachen.
Wie kann man den Scheitelpunkt einer Parabel bestimmen? Das wollen wir uns einmal an der Funktionsgleichung $k_b(x)=2x^2-4bx+3$ klarmachen.
- Es wird der Streckfaktor, also der Faktor vor dem $x^2$ ausgeklammert: $f(x)=2(x^2-2bx+1,5)$.
- Der Faktor vor dem $x$, also $-2b$, wird durch $2$ dividiert und dann wird das Vorzeichen vertauscht. So erhält man die x-Koordinate des Scheitelpunktes $x_s=b$.
- Die y-Koordinate erhält man, indem du $b$ in die Funktionsgleichung einsetzt: $y_S=2b^2-4b^2+3=-2b^2+3$.
Ausgehend von der Normalparabel ist diese Parabel
- um $b$ Einheiten entlang der x-Achse und
- um $-2b^2+3$ entlang der y-Achse verschoben.

Ortskurve (Ortslinie) bei Parabelscharen – Beispiele
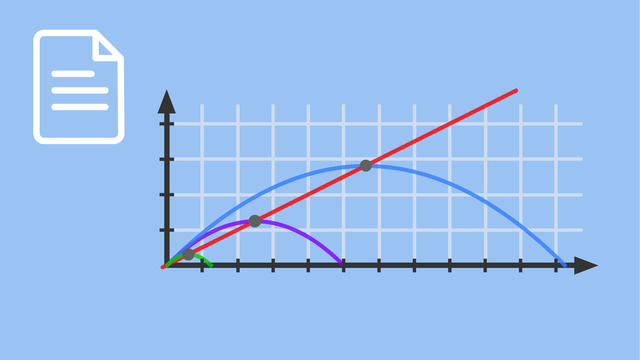
Ortskurve (Ortslinie) bei ganzrationalen Funktionen

Parabelscharen

Parabelscharen – Beispiele

Scharen von Wurzelfunktionen – Kurvendiskussion

Scharen von Exponentialfunktionen – Kurvendiskussion (1)

Scharen von Exponentialfunktionen – Kurvendiskussion (2)

Scharen von Logarithmusfunktionen – Kurvendiskussion

Schar von Winkelfunktionen – Kurvendiskussion
9'783
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'800
Lernvideos
37'168
Übungen
32'600
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?








