Gegenseitige Lage Punkt-Strecke und Punkt-Gerade

Inhaltsverzeichnis zum Thema

• Punkte
• Geraden im Raum
• Punktprobe

Punkte

Ein Punkt in der Ebene $\mathbb{R}^{2}$ oder im Raum $\mathbb{R}^{3}$ ist gegeben durch seine Koordinaten. So ist der Punkt $A(1|2)$ ein Punkt in der Ebene, er hat zwei Koordinaten, nämlich eine $x$- und eine $y$-Koordinate. Diese werden in mancher Literatur auch als $x_{1}$- und $x_{2}$-Koordinate bezeichnet. Der Punkt $B(2|2|4)$ liegt im Raum. Er hat drei Koordinaten, nämlich eine $x$-, eine $y$- sowie eine $z$-Koordinate. Auch hier wird oft die Schreibweise $x_{1}$, $x_{2}$ sowie $x_{3}$ verwendet.

Wir schauen uns im Folgenden den Raum $\mathbb{R}^{3}$ an. Solltest du Aufgaben in der Ebene bearbeiten müssen, läuft alles ganz genauso wie hier beschrieben, nur ohne $z$-Koordinate.

Geraden im Raum

Geraden sind entweder durch einen Punkt und einen Vektor oder durch zwei Punkte gegeben.

Eine Parametergleichung sieht so aus:

$g:\vec x=\vec a+r\cdot \vec u$

Dabei ist

• $\vec x$ ein Vektor, der auf einen beliebigen Punkt der Geraden zeigt,
• $\vec a$ ein Vektor, der auf einen gegebenen Punkt der Geraden zeigt, der Stützvektor,
• $\vec u$ der Richtungsvektor und
• $r\in\mathbb{R}$ ein Parameter.

Ein Punkt kann entweder auf einer Geraden liegen oder nicht: In dem folgenden Bild liegt $A$ auf der Geraden und $B$ nicht.

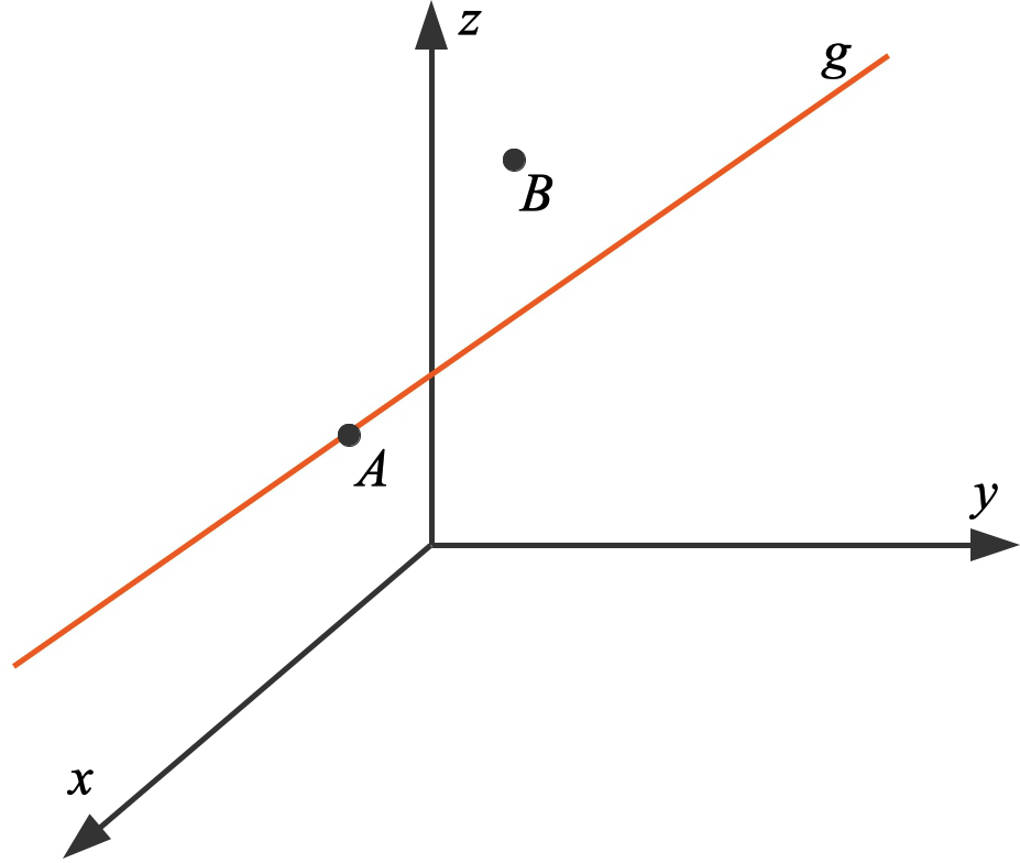
Wenn ein Punkt nicht auf einer Geraden liegt, kannst du den Abstand dieses Punktes zu der Geraden berechnen.

Punktprobe

Um zu prüfen, ob ein Punkt auf einer Geraden liegt, führst du eine Punktprobe durch. Du setzt hierfür den Ortsvektor des Punktes für $\vec x$ in die Geradengleichung ein. So erhältst du ein lineares Gleichungssystem mit drei Gleichungen und einer Unbekannten, dem Parameter.

Wir schauen uns dies an einem Beispiel an:

$g:\vec x=\begin{pmatrix} 1\\2\\1 \end{pmatrix}+r\cdot \begin{pmatrix} 1\\-1\\3 \end{pmatrix}$

Prüfe, ob der Punkt $A(2|2|3)$ auf dieser Geraden liegt. Setze den Ortsvektor von $A$ für $\vec x$ ein:

$\begin{pmatrix} 2\\2\\3 \end{pmatrix}=\begin{pmatrix} 1\\2\\1 \end{pmatrix}+r\cdot \begin{pmatrix} 1\\-1\\3 \end{pmatrix}$

Schau dir nun von oben nach unten die Gleichungen an:

$\begin{array}{rll} \text{I:} & 2 &=& 1+r \\ \text{II:} & 2 &=& 2-r \\ \text{III:} & 3 &=& 1+3r \end{array}$

Die Gleichung $\text{I}$ liefert $r=1$ und die Gleichung $\text{II}$ führt zu $r=0$.

Da du zwei verschiedene Lösungen für $r$ bekommst, ist das Gleichungssystem nicht lösbar. Der Punkt $A$ liegt also nicht auf der Geraden. Wenn er auf der Geraden liegt, löst ein Wert für $r$ alle drei Gleichungen.

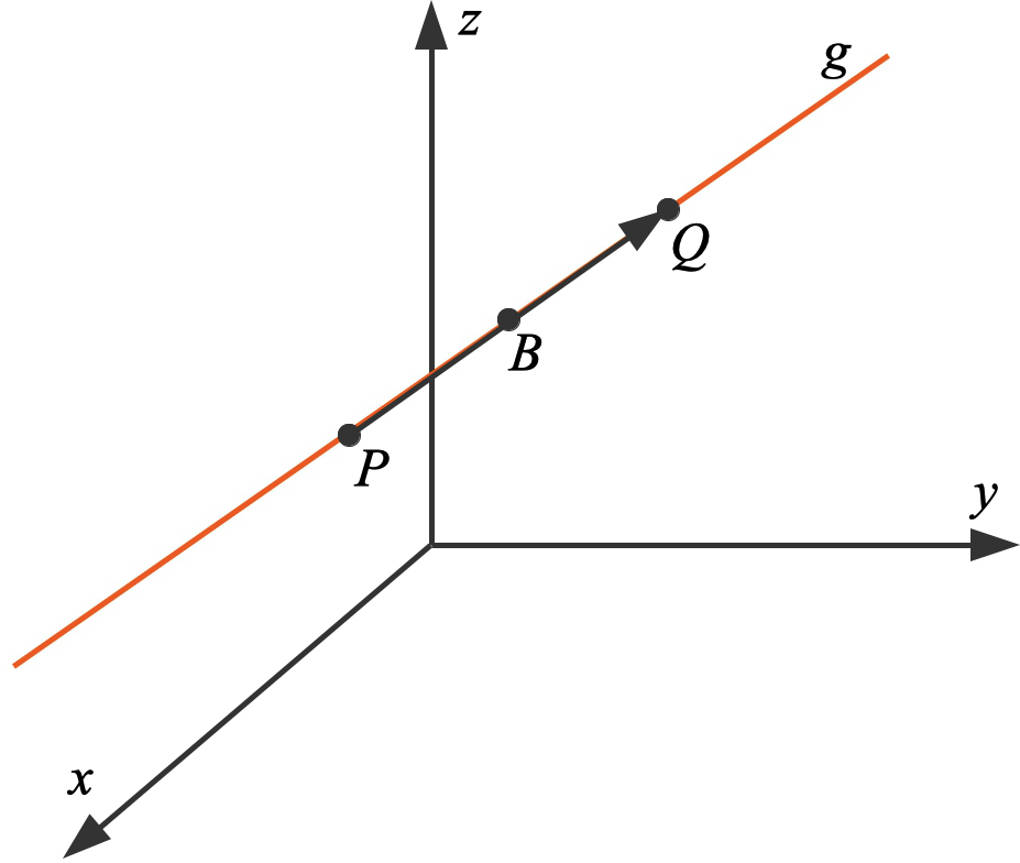
Dies schauen wir uns am Beispiel einer Zwei-Punkt-Gleichung einer Geraden durch die Punkte $P(2|1|4)$ sowie $Q(6|3|0)$ an. Der Richtungsvektor der Geraden ist der Verbindungsvektor der beiden Punkte und der Stützvektor der Ortsvektor eines der beiden Punkte:

$g:\vec x=\begin{pmatrix} 2\\1\\4 \end{pmatrix}+r\cdot \begin{pmatrix} 4\\2\\-4 \end{pmatrix}$

Nun sollst du die relative Lage des Punktes $B(4|2|2)$ prüfen. Die Punktprobe führt zu $r=0,5$. Der Punkt liegt also auf der Geraden.

Wir schauen uns die Bedeutung des Parameters $r$ bei einer Zwei-Punkt-Gleichung etwas genauer an: Wenn du wie in diesem Beispiel den Ortsvektor des Punktes $P$ als Stützvektor und den Verbindungsvektor von diesem Punkt aus zu dem anderen Punkt als Richtungsvektor verwendest, kannst du feststellen:

• $r=0$ führt zu dem Punkt $P$.
• $r=1$ führt zu dem Punkt $Q$.
• $0<r<1$ bedeutet,="" dass="" der="" punkt="" auf="" strecke="" $\overline{pq}$="" liegt.="" in="" dem="" obigen="" beispiel="" liegt="" genau="" mitte="" strecke:="" " ##="" abstandsberechnung="" wie="" bereits="" erwähnt,="" kannst="" du="" für="" einen="" $a$,="" welcher="" nicht="" einer="" geraden="" liegt,="" den="" abstand="" dieses="" punktes="" zu="" berechnen.="" dabei="" verschiedene="" vorgehensweisen="" behandeln:="" *="" verwendest="" das="" lotfußpunktverfahren:="" mit="" hilfe="" ebene,="" welche="" senkrecht="" betrachteten="" $g$="" und="" $a$="" enthält,="" lotfußpunkt="" bestimmen.="" dies="" ist="" schnittpunkt="" hilfsebene="" geraden.="" gesuchte="" abstand="" dann="" des="" diesem="" schnittpunkt.="" verbindungsvektor="" von="" einem="" beliebigen="" aufstellen.="" darin="" kommt="" parameter="" $r$="" vor.="" nun="" bestimmst="" so,="" dieser="" richtungsvektor="" steht.="" schließlich="" auch="" hängt="" ab.="" da="" man="" mathematik="" unter="" immer="" kürzesten="" versteht,="" minimalen="" abstand.="" hierfür="" quadrierten="" abhängigkeit="" leitest="" diesen="" die="" erste="" ableitung="" muss="" $0$="" sein.="" mittlere="" verfahren="" schauen="" wir="" uns="" abschließend="" noch="" anfängliche="" an.="" bestimme="" verbindungsvektor="" <p=""> $\vec{P_{g}A}=\begin{pmatrix} 1-r\r\2-3r \end{pmatrix}$

Bestimme $r$

Der obige Vektor muss senkrecht zu dem Richtungsvektor sein. Zwei Vektoren sind senkrecht, wenn deren Skalarprodukt gleich $0$ ist. Dies führt zu der folgenden Gleichung:

$1-r-r+3(2-3r)=0~\Leftrightarrow~7-11r=0~\Leftrightarrow~r=\frac{7}{11}$

Nun setzt du diesen Wert für $r$ in die Geradengleichung ein und erhältst den Punkt mit dem kürzesten Abstand zu $A$. Der Abstand von $A$ zu der Geraden ist dann der Abstand der beiden Punkte zueinander.</r<1$>