Additionstheoreme für sin(x+y) und cos(x+y)

Inhaltsverzeichnis zum Thema

• Die Definition von Sinus und Cosinus in einem rechtwinkligen Dreieck.
• 1. und 2. Additionssatz
• 1. Additionssatz
• 2. Additionssatz
• 3. und 4. Additionssatz
• Anwendung der Additionssätze
• $\sin(2\alpha)$
• $\cos(2\alpha)$

Die Definition von Sinus und Cosinus in einem rechtwinkligen Dreieck.

Der Sinuswert eines spitzen Winkels in einem rechtwinkligen Dreieck ist der Quotient aus der Länge der Gegenkathete dieses Winkels sowie der Länge der Hypotenuse.

$~~$

Der Kosinuswert ist definiert als der Quotient aus der Länge der Ankathete dieses Winkels sowie der der Hypotenuse. Es gilt:

• $\sin(\alpha)=\frac{\text{Gegenkathete von }\alpha}{\text{Hypotenuse}}$
• $\cos(\alpha)=\frac{\text{Ankathete von }\alpha}{\text{Hypotenuse}}$

Die Sinus- sowie Kosinusfunktion werden trigonometrische Funktionen oder auch Winkelfunktionen genannt.

Es gilt der trigonometrische Pythagoras $(\sin(\alpha))^2+(\cos(\alpha))^2=1$. Dies kannst du dir am Einheitskreis klarmachen.

Damit kannst du schon Sinus- oder Kosinuswerte für bestimmte Winkel berechnen. Zum Beispiel ist $\sin(45^\circ)=\cos(45^\circ)$, da ein rechtwinkliges Dreieck mit übereinstimmenden Basiswinkeln gleichschenklig ist. Dann erhältst du:

$\begin{array}{rrcll}~&(\sin(45^\circ))^2+(\cos(45^\circ))^2&=&1& \vert~\cos(45^\circ)=\sin(45^\circ)\\ \Leftrightarrow & (\sin(45^\circ))^2+(\sin(45^\circ))^2 & = & 1 &~\\ \Leftrightarrow & 2\cdot(\sin(45^\circ))^2 & = & 1 & \vert~:2\\ \Leftrightarrow & (\sin(45^\circ))^2 & = & \frac12 & \vert \sqrt{}\\ \Leftrightarrow & \sin(45^\circ) & = & \sqrt{\frac12} &~\\ \Leftrightarrow & \sin(45^\circ) & \approx & 0,707 &~ \end{array}$

Somit gilt:

$\sin(45^\circ)=\cos(45^\circ)=\frac1{\sqrt2}\approx 0,707$

. Kosinuswerte sind beispielsweise gegeben durch:

• $\sin(30^\circ)=0,5$
• $\sin(60^\circ)=\frac{\sqrt 3}2$
• $\cos(30^\circ)=\frac{\sqrt 3}2$
• $\cos(60^\circ)=0,5$

Wie können Sinus- und Kosinuswerte von Summen oder Differenzen von Winkeln berechnet werden?

Hierfür werden die Additionssätze verwendet.

1. und 2. Additionssatz

1. Additionssatz

Der 1. Additionssatz lautet:

$\sin(\alpha+\beta)=\sin(\alpha)\cdot\cos(\beta)+\cos(\alpha)\cdot\sin(\beta)$

.

Nachweis dieses Satzes

Schaue dir dieses Dreieck an:

.

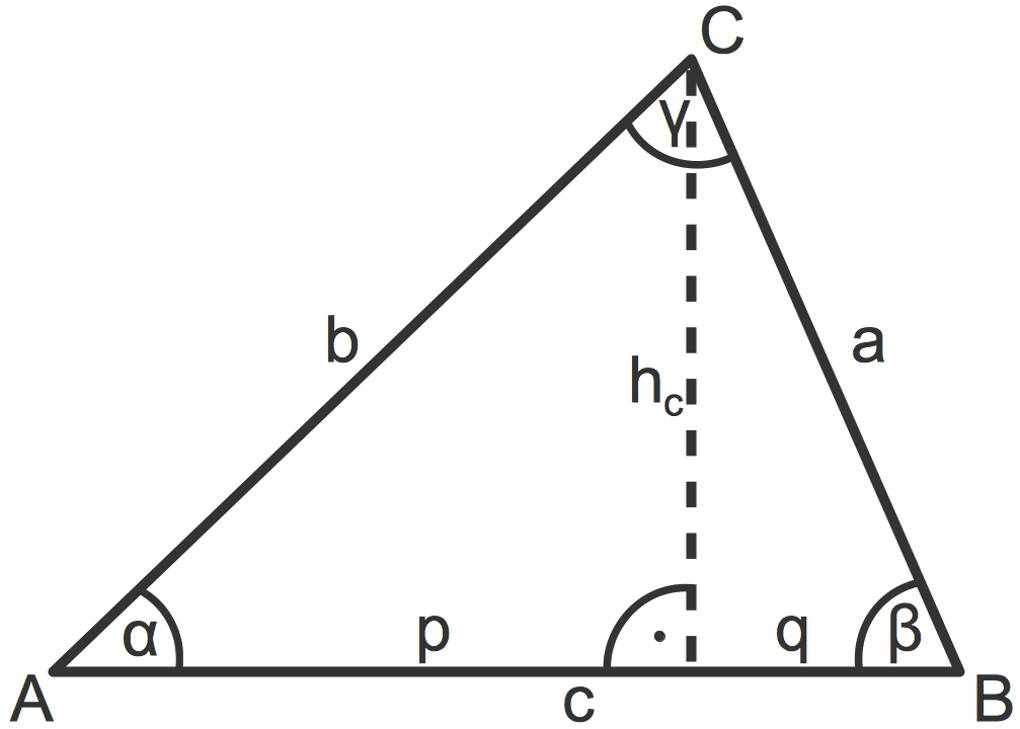• Mit dem Sinussatz gilt:

$\quad~~~\frac{\sin(\gamma)}{c}=\frac{\sin(\alpha)}{a}$

.

• Multiplikation mit $c$ führt zu:

$\quad~~~\sin(\gamma)=\frac{\sin(\alpha)\cdot c}{a}$

.

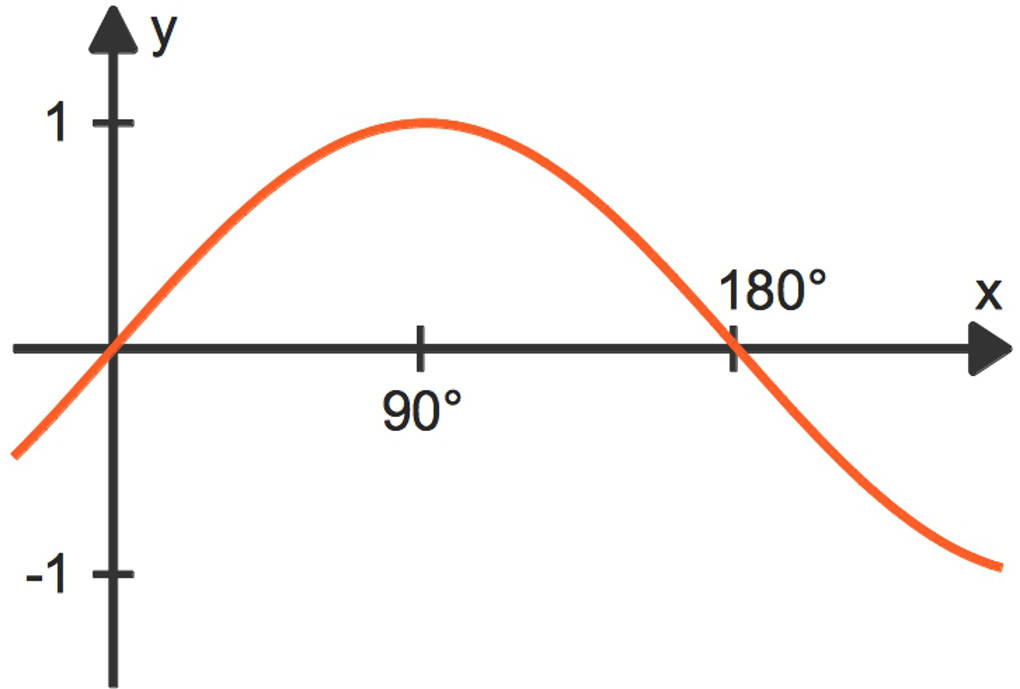
• Mit dem Winkelsummensatz gilt $\alpha+\beta+\gamma=180^\circ$. Nun subtrahierst du $\alpha+\beta$ zu $\gamma=180^\circ-(\alpha+\beta)$. Da die Sinusfunktion symmetrisch zu einer zur y-Achse parallelen Geraden durch $x=90^\circ$ ist, folgt: $\sin(\gamma)=\sin(180^\circ-(\alpha+\beta))=\sin(\alpha+\beta)$.

• Nun verwendest du $c=p+q$ und erhältst

$\quad~~~\begin{array}{rcl}\sin(\alpha+\beta)&=&\frac{\sin(\alpha)\cdot (p+q)}{a}\\ &=&\frac{\sin(\alpha)\cdot p}{a}+\frac{\sin(\alpha)\cdot q}{a}\\ &=&\frac{ \sin(\alpha)} a\cdot p +\sin(\alpha)\cdot \frac qa\end{array}$

• $a$ ist die Hypotenuse in dem rechten rechtwinkligen Dreieck und $q$ die Ankathete von $\beta$, also ist:

$\quad~~~\frac qa=\cos(\beta)$

.

• Dies kannst du in der obigen Gleichung einsetzen

$\quad~~~\sin(\alpha+\beta)=\frac{ \sin(\alpha)} a\cdot p+\sin(\alpha)\cdot \cos(\beta)$

.

• Du siehst, da steht bereits ein Teil des 1. Additionssatzes.
• Du verwendest noch einmal den Sinussatz

$\quad~~~\frac{\sin(\alpha)}{a}=\frac{\sin(\beta)}{b}$

.

• Nun setzt du dies in die Gleichung ein

$\quad~~~\begin{array}{rcl}\sin(\alpha+\beta)&=&\frac{\sin(\beta)}{b}\cdot p+\sin(\alpha)\cdot \cos(\beta)\\ &=&\sin(\beta)\cdot \frac pb+\sin(\alpha)\cdot \cos(\beta)\end{array}$

• In dem linken rechtwinkligen Dreieck gilt

$\quad~~~\frac pb=\cos(\alpha)$

.

• Damit ist der Additionssatz bewiesen

$\quad~~~\sin(\alpha+\beta)=\sin(\beta)\cdot \cos(\alpha)+\sin(\alpha)\cdot \cos(\beta)$

.

• Du musst nur noch die Reihenfolge der Addition sowie Multiplikation umstellen und schon bist du fertig.

Beispiel: Nun kannst du den Sinuswert, zum Beispiel des Winkels $75^\circ$, berechnen. Diesen erhältst du mit dem Taschenrechner $\sin(75^\circ)\approx 0,966$:

$\begin{array}{rcl}\sin(75^\circ)&=&\sin(45^\circ+30^\circ)\\ &=&\sin(45^\circ)\cdot\cos(30^\circ)+\cos(45^\circ)\cdot\sin(30^\circ)\\ &=&\frac1{\sqrt2}\cdot\frac{\sqrt 3}2+\frac1{\sqrt 2}\cdot 0,5 \\ &=&\frac{\sqrt 3+1}{2\sqrt 2}\\ &\approx&0,966 \end{array}$

2. Additionssatz

Der 2. Additionssatz lautet

$\sin(\alpha-\beta)=\sin(\alpha)\cdot\cos(\beta)-\cos(\alpha)\cdot\sin(\beta)$

Nachweis dieses Satzes

• Es ist $\sin(\alpha-\beta)=\sin(\alpha+(-\beta))$. Nun kannst du den 1. Additionssatz verwenden:

$\quad~~~\sin(\alpha+(-\beta))=\sin(\alpha)\cdot\cos(-\beta)+\cos(\alpha)\cdot\sin(-\beta)$

.

• Die Cosinusfunktion ist achsensymmetrisch, also ist $\cos(-\beta)=\cos(\beta)$, und die Sinusfunktion punktsymmetrisch, also ist $\sin(-\beta)=-\sin(\beta)$.
• Damit gilt $\sin(\alpha-\beta)=\sin(\alpha)\cdot\cos(\beta)-\cos(\alpha)\cdot\sin(\beta)$.
• Dies ist der 2. Additionssatz.

Beispiel: Berechne $\sin(15^\circ)$. Mit dem Taschenrechner erhältst du $\sin(15^\circ)\approx 0,259$.

$\begin{array}{rcl}\sin(15^\circ)&=&\sin(45^\circ-30^\circ)\\ &=&\sin(45^\circ)\cdot\cos(30^\circ)-\cos(45^\circ)\cdot\sin(30^\circ)\\ &=&\frac1{\sqrt2}\cdot\frac{\sqrt 3}2-\frac1{\sqrt 2}\cdot 0,5 \\ &=&\frac{\sqrt 3-1}{2\sqrt 2}\\ &\approx&0,259 \end{array}$

3. und 4. Additionssatz

Der 3. Additionssatz lautet

$\cos(\alpha+\beta)=\cos(\alpha)\cdot\cos(\beta)-\sin(\alpha)\cdot\sin(\beta)$

.

Beispiel: Berechne $\cos(75^\circ)$. Hier erhältst du mit dem Taschenrechner$\cos(75^\circ)\approx0,259$.

$\begin{array}{rcl}\cos(75^\circ)&=&\cos(45^\circ+30^\circ)\\ &=&\cos(45^\circ)\cdot\cos(30^\circ)-\sin(45^\circ)\cdot\sin(30^\circ)\\ &=&\frac1{\sqrt2}\cdot\frac{\sqrt 3}2-\frac1{\sqrt 2}\cdot 0,5 \\ &=&\frac{\sqrt 3-1}{2\sqrt 2}\\ &\approx&0,259 \end{array}$

Der 4. Additionssatz lautet

$\cos(\alpha-\beta)=\cos(\alpha)\cdot\cos(\beta)+\sin(\alpha)\cdot\sin(\beta)$

.

Beispiel: Berechne $\cos(15^\circ)$. Gib dies in den Taschenrechner ein. Du erhältst $\cos(15^\circ)\approx0,966$.

$\begin{array}{rcl}\cos(15^\circ)&=&\cos(45^\circ-30^\circ)\\ &=&\cos(45^\circ)\cdot\cos(30^\circ)+\sin(45^\circ)\cdot\sin(30^\circ)\\ &=&\frac1{\sqrt2}\cdot\frac{\sqrt 3}2+\frac1{\sqrt 2}\cdot 0,5 \\ &=&\frac{\sqrt 3+1}{2\sqrt 2}\\ &\approx&0,966 \end{array}$

Anwendung der Additionssätze

• Du kannst mit den Additionssätzen (bei bekannten Sinus- und Cosinuswerten) die Sinus- und Kosinuswerte von zusammengesetzten Winkeln berechnen.
• Du kannst auch Sinus- oder Kosinuswerte von Vielfachen von Winkeln berechnen.

$\sin(2\alpha)$

• Da $2\alpha=\alpha+\alpha$ ist, gilt

$\quad~~~\sin(2\alpha)=\sin(\alpha+\alpha)$.

.

• Nun kannst du den 1. Additionssatz anwenden:

$\quad~~~\sin(\alpha+\alpha)=\sin(\alpha)\cdot\cos(\alpha)+\cos(\alpha)\cdot\sin(\alpha)=2\sin(\alpha)\cdot \cos(\alpha)$

.

Auch damit kannst du spezielle Sinuswerte berechnen:

$\begin{array}{rcl}\sin(120^\circ)&=&\sin(2\cdot 60^\circ)\\ &=&2\sin(60^\circ)\cdot \cos(60^\circ)\\ &=&2\cdot \cdot \frac{\sqrt 3}2\cdot\frac12\\ &=&\frac{\sqrt 3}2\\ &\approx&0,866\end{array}$

$\cos(2\alpha)$

• Hier verwendest du wieder $2\alpha=\alpha+\alpha$:

$\quad~~~\cos(2\alpha)=\cos(\alpha+\alpha)$

.

• Nun kannst du den 3. Additionssatz anwenden:

$\quad~~~\cos(\alpha+\alpha)=\cos(\alpha)\cdot\cos(\alpha)-\sin(\alpha)\cdot\sin(\alpha)=(\cos(\alpha))^2-(\sin(\alpha))^2$

.

• Mit dem trigonometrischen Pythagoras kannst du weiter umformen zu:

$\quad~~~\begin{array}{rcl} \cos(\alpha+\alpha)&=&(\cos(\alpha))^2-(\sin(\alpha))^2\\ &=&(\cos(\alpha))^2-(1-\cos(\alpha))^2\\ &=&2(\cos(\alpha))^2-1 \end{array}$