Extremwertaufgaben, Mittelwertsatz und Newton-Verfahren
Ein Extremwert ist der Oberbegriff für ein lokales und globales Maximum und Minimum.
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Was ist eine Extremwertaufgabe?
- Allgemeines Vorgehen bei Extremwertaufgaben
- Beispiel: Flächenmaximales Rechteck
- Aufstellen der Hauptbedingung
- Aufstellen der Nebenbedingung
- Umformen der Nebenbedingung nach einer der beiden Variablen
- Aufstellen der Zielfunktion
- Ermitteln der Extrema
Was ist eine Extremwertaufgabe?
Stelle dir das folgende Beispiel vor: Du hast insgesamt $200~m$ Zaun zu Verfügung. Damit sollst du ein Rechteck mit möglichst großem Flächeninhalt abgrenzen.
Du kannst natürlich verschiedene Rechtecke konstruieren und schauen, welches den größten Flächeninhalt hat. Dies ist allerdings kein sehr mathematisches Vorgehen. Abgesehen davon, kannst du dir nicht sicher sein, die optimale Lösung gefunden zu haben.
In der Aufgabenstellung kommt möglichst groß vor. Hier soll also etwas maximal werden. Woran denkst du dann? Richtig, an die Differentialrechnung. Wenn etwas möglichst groß oder möglichst klein werden soll, bestimmst du Extrema. Hierfür untersuchst du die notwendige sowie die hinreichende Bedingung für Extrema.
Eine solche Aufgabe wird als Extremwertaufgabe, Extremwertproblem oder als Extremalaufgabe bezeichnet.
Bei dieser Aufgabe sind zwei Größen unbekannt: Die Länge und die Breite des Rechtecks.
Allgemeines Vorgehen bei Extremwertaufgaben
Zum Lösen von Extremwertaufgaben gehst du wie folgt vor:
- Du formulierst eine Hauptbedingung: Was muss möglichst groß oder möglichst klein werden?
- Wenn zwei Größen, wie in dem obigen Beispiel, vorkommen, musst du eine Nebenbedingung aufstellen: Welcher Zusammenhang zwischen den beiden Größen ist gegeben?
- Diese Nebenbedingung stellst du nach einer der beiden unbekannten Größen um.
- Nun setzt du die umgestellte Nebenbedingung in der Hauptbedingung ein. Die Hauptbedingung hängt nun nur noch von einer Größe ab. Die so erhaltene Funktion wird als Zielfunktion bezeichnet.
- Abschließend kannst du diese Zielfunktion zweimal ableiten und mit Hilfe der notwendigen sowie hinreichenden Bedingung die Extrema herausfinden.
Beispiel: Flächenmaximales Rechteck
Lass uns dieses Vorgehen einmal an einem Beispiel üben:
Aufstellen der Hauptbedingung
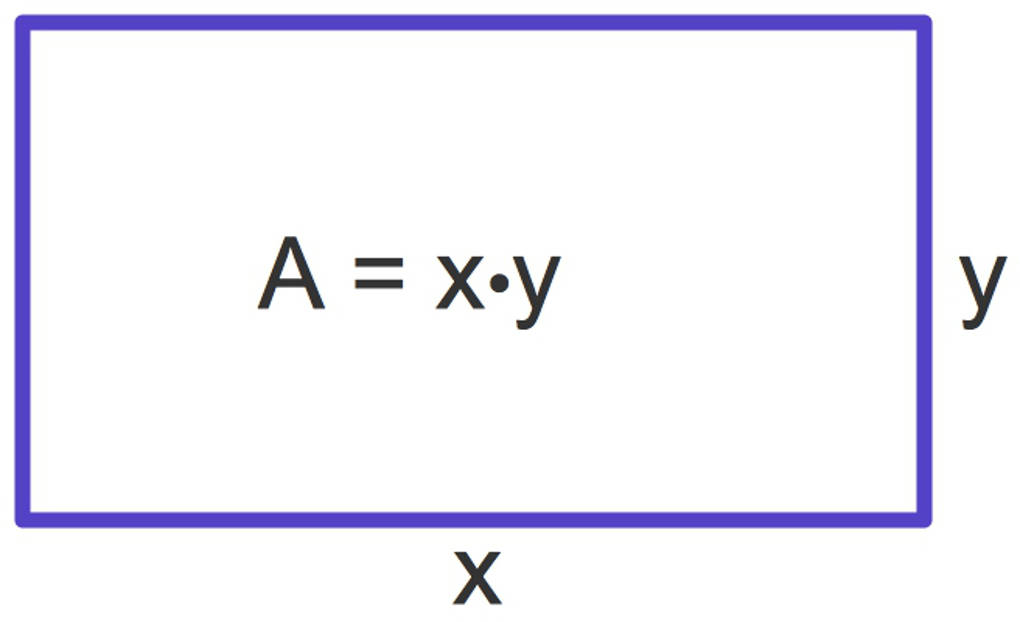
Der Flächeninhalt eines Rechtecks ist gegeben durch Länge mal Breite. Beide Größen sind unbekannt, also weist du diesen Größen Variablen, zum Beispiel $x$ und $y$, zu.
Der Flächeninhalt $A(x,y)=x\cdot y$ hängt somit von zwei Variablen ab. Die Fläche $A(x,y)$ soll maximiert werden.
Aufstellen der Nebenbedingung
Du weißt, wie Extrema von Funktionen mit einer Veränderlichen bestimmt werden. Um eine solche Funktion zu erhalten, musst du den Zusammenhang zwischen den beiden Variablen formulieren. Es ist bekannt, dass der Umfang des Rechtecks, also die gesamte Länge des Zauns, $200~m$ beträgt. Dies führt unter Verwendung der Formel für den Umfang von Rechtecken zu der Nebenbedingung $2x+2y=200$.
Umformen der Nebenbedingung nach einer der beiden Variablen
Es ist egal, nach welcher der beiden Variablen du die Nebenbedingung umstellst.
$\begin{array}{rclll} 2x+2y&=&200&|&-2x\\ 2y&=&200-2x&|&:2\\ y&=&100-x \end{array}$
Aufstellen der Zielfunktion
Nun kannst du diese Gleichung ($y=100-x$) in die Hauptbedingung ($A(x,y)=x\cdot y$) einsetzen und erhältst die Zielfunktion
$f(x)=x\cdot (100-x)=100x-x^2=-x^2+100x$
.
Ermitteln der Extrema
Zur Bestimmung der Extrema der Zielfunktion berechnest du erst einmal deren erste sowie zweite Ableitung:
$\begin{array}{rll} f(x)&=&-x^2+100x\\ f'(x)&=&-2x+100\\ f''(x)&=&-2 \end{array}$
Es gelten die folgenden Bedingungen für Extrema:
- notwendige Bedingung $f'(x_E)=0$
- hinreichende Bedingung $f'(x_E)$ und $f''(x_E)\neq 0$. Durch das Vorzeichen der zweiten Ableitung kannst du bestimmen, welcher Art das Extremum ist: Es liegt ein (lokales) Minimum (Tiefpunkt) vor, wenn $f''(x_E)>0$ ist und ein (lokales) Maximum (Hochpunkt), wenn $f''(x_E)<0$ ist.
$f'(x_E)=0$ führt zu $-2x_E+100=0$. Nun subtrahierst du $100$ und dividierst anschließend durch $-2$. So erhältst du $x_E=50$.
Nun setzt du diesen Wert für $X_E$ in der zweiten Ableitung ein: $f''(x_E)=f''(50)=-2<0$. Es liegt also ein Maximum (Hochpunkt) vor.
Da $y=100-x$ ist, kannst du mit $x_E=50$ auch den $y$-Wert berechnen: $y_E=100-x_E=100-50=50$.
Das flächenmaximale Rechteck mit einem Umfang von $200~m$ ist damit ein Quadrat mit den Seitenlängen $50~m$ und dem Flächeninhalt $A=(50~m)^2=2500~m^2$.
Beispiel: Fußballstadion
Hier siehst du ein weiteres Beispiel:
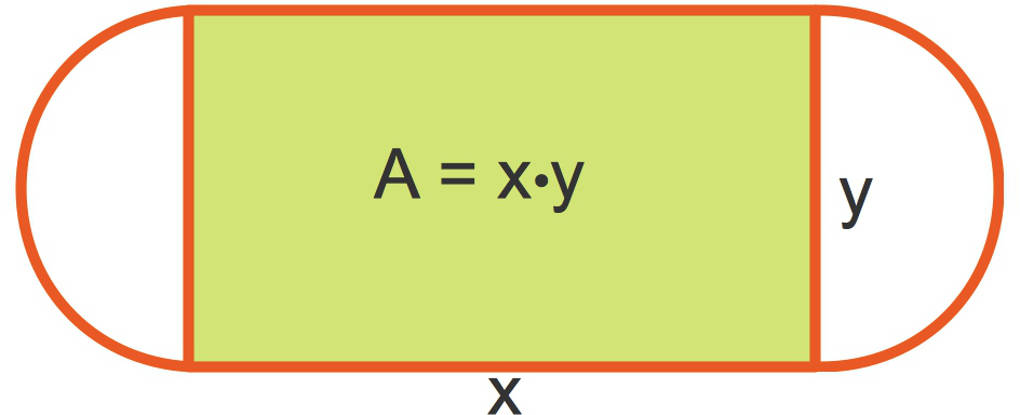
Es soll ein Fußballplatz gebaut werden. Das rechteckige Spielfeld soll einen möglichst großen Flächeninhalt haben. Eine Laufbahn (Tartanbahn) der Länge $400~m$ umgibt das Spielfeld. Diese Bahn besteht aus zwei Halbkreisen sowie zwei Seiten des Spielfeldes. Du kannst dies in dem obigen Bild sehen.
- Hauptbedingung: $~~A(x,y)=x\cdot y\rightarrow \text{max}$
- Nebenbedingung: $~~2x+\pi y=400$
- Umformen der Nebenbedingung: $~~x=200-\frac{\pi}{2}y$
- Einsetzen von $x$ in $A(x,y)$: $~~\left(200-\frac{\pi}{2}y\right)\cdot y=-\frac{\pi}2y^2+200y$
- Zielfunktion: $~~f(y)=-\frac{\pi}2y^2+200y$
- Ableitungen: $~~f'(y)=-\pi y+200$ und $f''(y)=-\pi$
- notwendige Bedingung: $~~f'(y_E)=0$ führt zu $y_E=\frac{200}{\pi}\approx 63,66$
- hinreichende Bedingung: $~~f''(y_E)=-\pi<0$. Es liegt also ein Maximum vor.
Nun muss noch $x_E$ und der maximale Flächeninhalt $A_{\text{max}}$ berechnet werden:
$x_E=200-\frac{\pi}{2}\cdot \frac{200}{\pi}=100$
$A_{\text{max}}=63,66~m\cdot 100~m=6366~m^2$
Das Spielfeld mit dem maximalen Flächeninhalt $6366~m^2$ hat die Maße $x_E=100~m$ sowie $y_E=63,66~m$.
Der Mittelwertsatz
Der Mittelwertsatz ist ein Satz der Differentialrechnung, welche sich mit den Ableitungen von Funktionen befasst. Der Mittelwertsatz dient dazu, Punkte auf einer Funktion mit einer bestimmten Steigung zu finden. Er gilt nur unter bestimmten Voraussetzungen. Werden diese nicht erfüllt, kannst du Gegenbeispiele finden, in welchen die Aussage des Mittelwertsatzes nicht zutrifft.
Die Voraussetzungen
Betrachtet wird eine Funktion $f$ sowie der Graph dieser Funktion $G_{f}$ auf dem Intervall $[a;b]$ mit $a\neq b$. Es muss gelten:
- Die Funktion $f$ ist stetig auf dem abgeschlossenen Intervall $[a;b]$.
- Weiter muss $f$ differenzierbar auf dem offenen Intervall $(a;b)$ sein.
Die Aussage
Unter den obigen Voraussetzungen gilt dann: Es existiert mindestens ein $x_{0}\in(a;b)$ mit
$f'\left(x_{0}\right)=\dfrac{f(b)-f(a)}{b-a}$.
Der Mittelwertsatz anschaulich
Was bedeutet diese Aussage anschaulich? Schau dir das folgende Bild an:
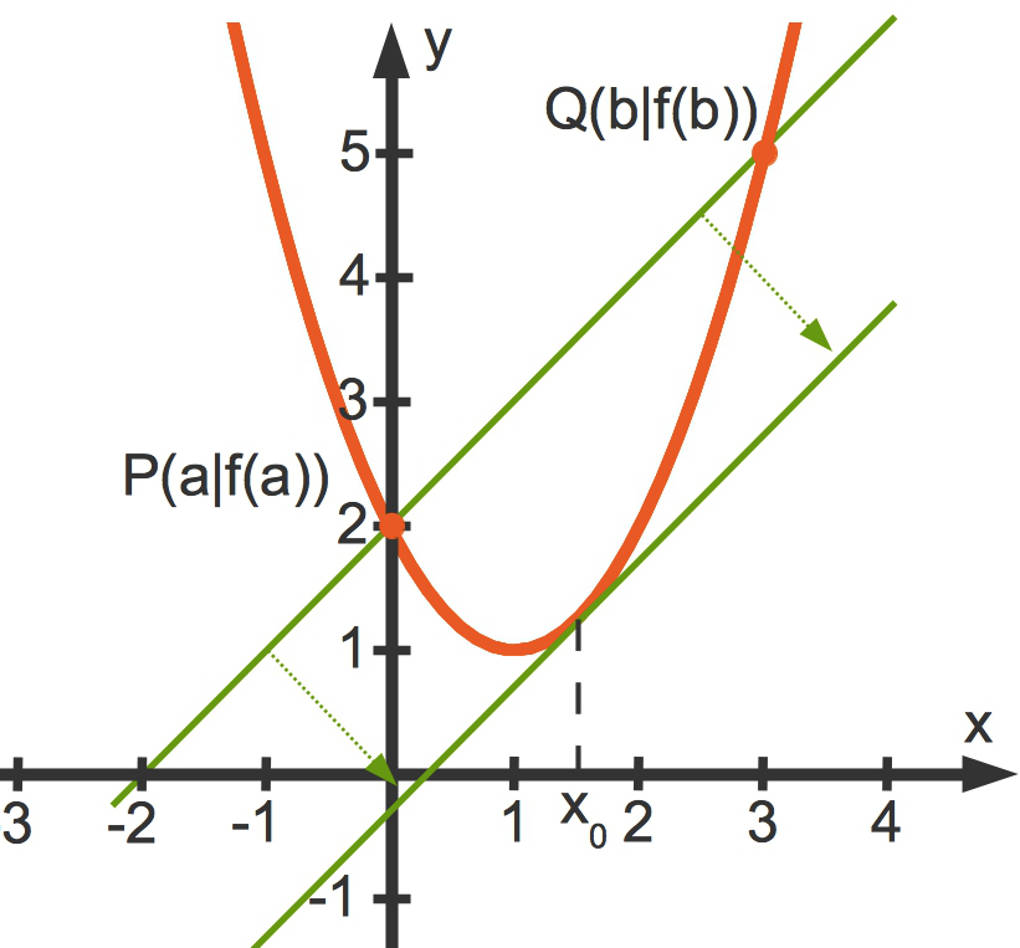
- Wenn du die Punkte $P(a|f(a))$ sowie $Q(b|f(b))$ miteinander verbindest, erhältst du eine Sekante. Dies ist eine Gerade, welche den Graphen $G_{f}$ schneidet. Die Steigung der Sekante ist $\frac{f(b)-f(a)}{b-a}$.
- Verschiebst du nun diese Sekante parallel, so berührt die parallel verschobene Gerade irgendwann $G_{f}$. Du erhältst also eine Tangente. Die Steigung der Tangente ist $f'\left(x_{0}\right)$.
- Da die Tangente durch Parallelverschiebung aus der Sekante hervorgeht, haben die beiden Geraden die gleiche Steigung.
So erhältst du die obige Aussage des Mittelwertsatzes.
Ein Beispiel für die Verletzung einer Voraussetzung:
Wenn zum Beispiel die Funktion $f$ nicht auf dem gesamten Intervall $[a;b]$ stetig ist, kannst du Folgendes beobachten. Hier siehst du einen Funktionsgraphen $G_{f}$ einer nicht stetigen Funktion $f$. Der Funktionsgraph hat eine Sprungstelle.
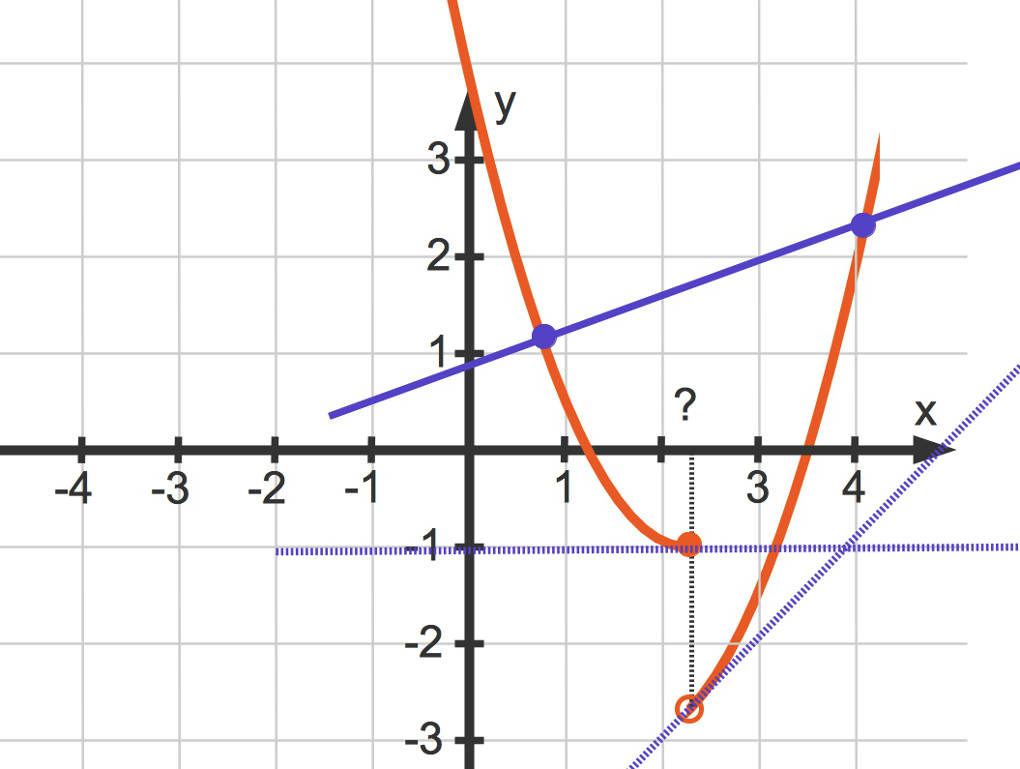
Du kannst erkennen, dass die Steigung $f'(x_0)=0$ ist. Diese ist jedoch nicht die Steigung der parallel verschobenen Sekante.
Der Satz von Rolle
Der Satz von Rolle ist ein Spezialfall des Mittelwertsatzes. Es gelten die gleichen Voraussetzungen wie beim Mittelwertsatz. Zusätzlich wird noch verlangt, dass die Funktionswerte an den Intervallrändern übereinstimmen, also $f(a)=f(b)$. Daraus folgt, dass die resultierende Sekante eine zur $x$-Achse parallele Gerade ist und damit die Steigung $0$ hat.
Die Aussage
Unter den obigen Vorraussetzungen gilt: Es existiert mindestens ein $x_{0}\in(a;b)$ mit $f'\left(x_{0}\right)=0$.
Der Satz von Rolle anschaulich
Auch hierzu schaue dir zunächst das folgende Bild an:
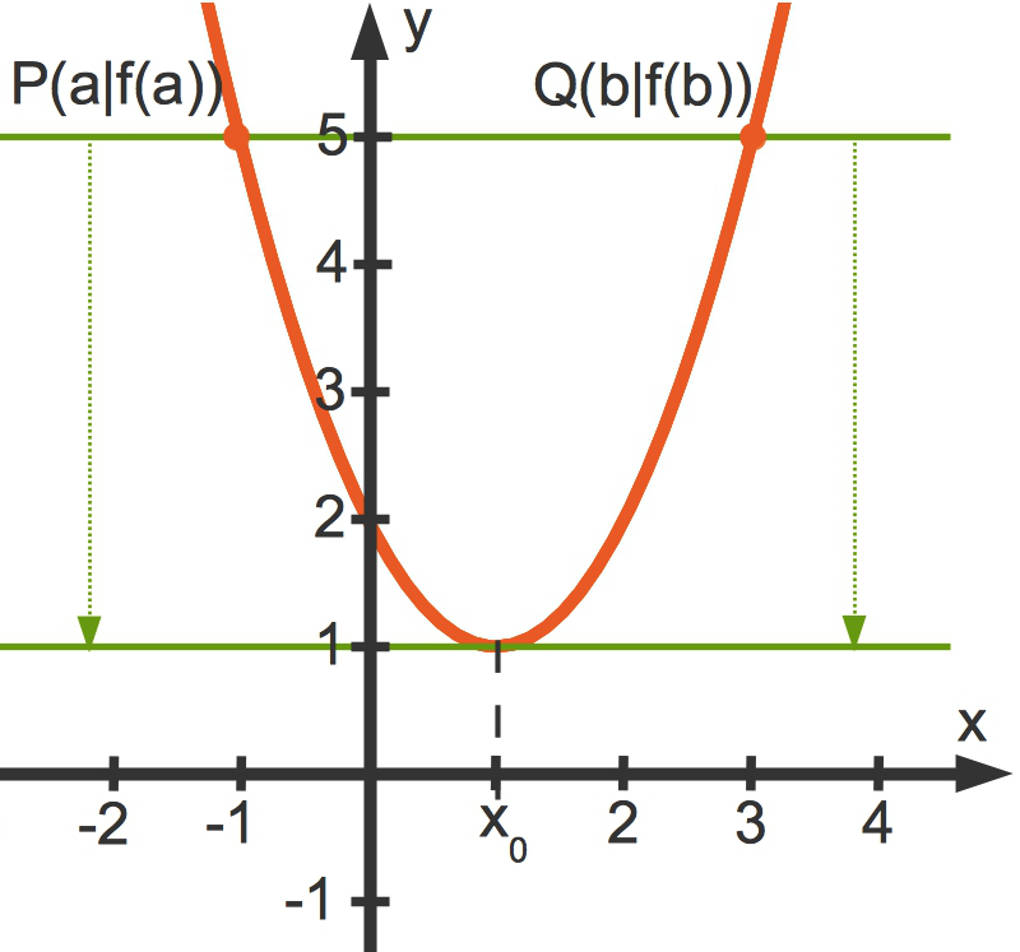
- Wie bereits festgestellt, hat die Sekante durch die Punkte $P(a|f(a))$ sowie $Q(b|f(b))$ die Steigung $0$.
- Die durch Parallelverschiebung entstandene Tangente hat dann ebenfalls die Steigung $0$.
Was ist so wichtig an dem Satz von Rolle?
Eine Stelle mit der Steigung $0$ ist eine mögliche Extremstelle. Wie du an dem obigen Bild erkennen kannst, liegt in diesem Beispiel auch tatsächlich eine Extremstelle vor. Die Aussage des Satzes von Rolle kannst du zum Beispiel im Zusammenhang mit Extremwertaufgaben verwenden.
Was ist das Newton-Verfahren?
Wenn du Nullstellen berechnen willst, helfen dir häufig diese klassischen Methoden:
- Die Nullstellen einer linearen Funktion erhältst du durch Äquivalenzumformungen.
- Die Nullstellen einer quadratischen Funktion berechnest du mit der p-q-Formel.
- Um die Nullstellen einer kubischen Funktion zu bestimmen, musst du eine Nullstelle raten und dann eine Polynomdivision durchführen. Das funktioniert jedoch nur, wenn eine Nullstelle ganzzahlig ist.
Wie kannst du die Nullstellen einer kubischen Funktion finden, wenn keine Nullstelle ganzzahlig ist? Du verwendest das Newton-Verfahren.
Das Newton-Verfahren, auch Tangentenverfahren genannt, ist ein iteratives Verfahren zur approximativen Bestimmung von Nullstellen. Es geht also um die Näherungen von Nullstellen.
Die Grundidee: Wir legen eine Tangente im Punkt $P(x_0|y_0=f(x_0))$ an die nichtlineare Funktion an. $x_0$ wird als Startwert bezeichnet. Dann wird die Nullstelle $x_1$ dieser Tangenten bestimmt. Im Koordinatensystem ist dieser erste Schritt abgebildet.
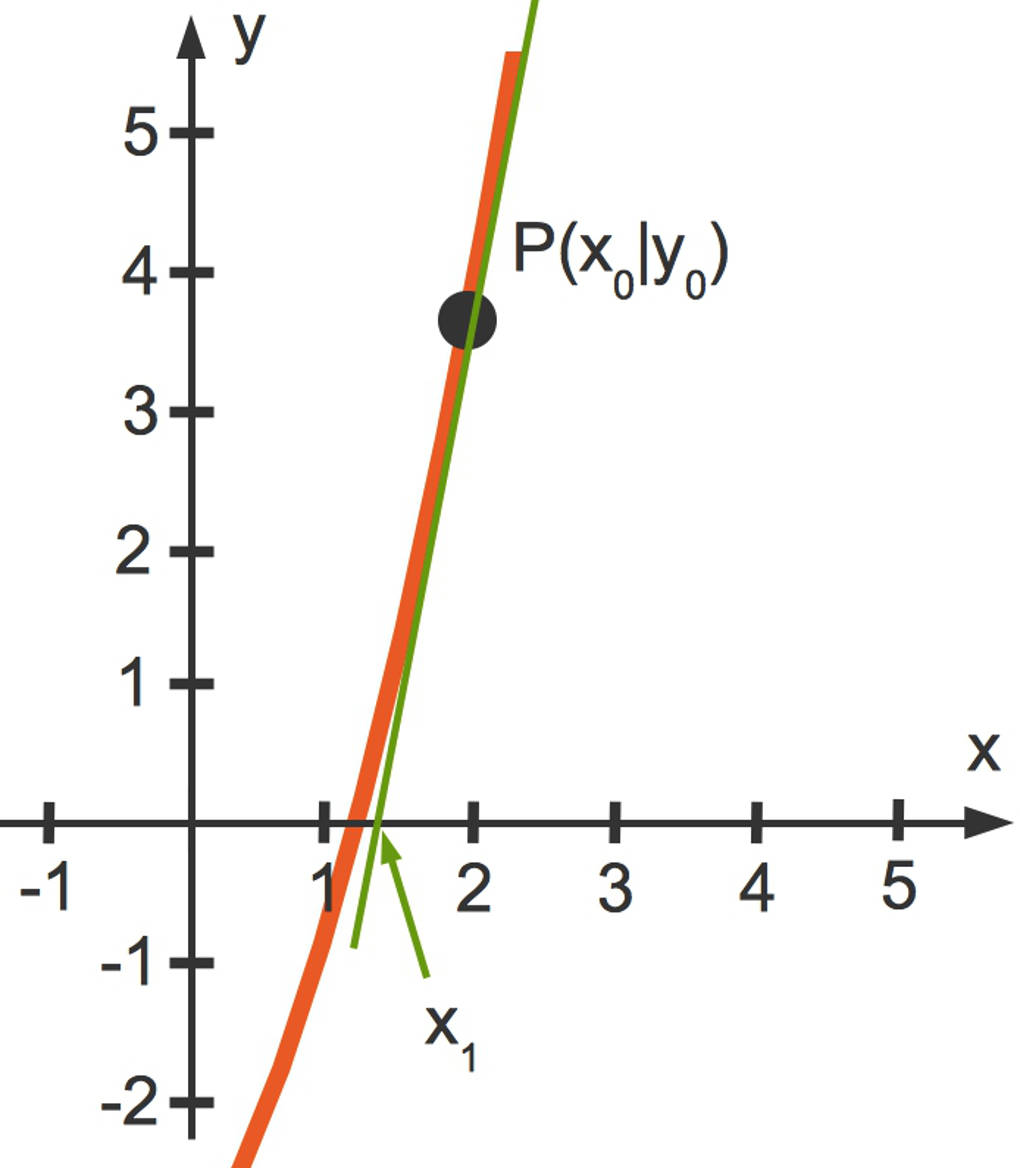
Dann wiederholen wir diesen Schritt (daher heißt es ja auch ein iteratives Verfahren). Wir legen diesmal die Tangente im Punkt $P(x_1|y_1)$ an die nichtlineare Funktion an. Die Nullstelle dieser Tangente wird dann $x_2$ genannt.
So fährt man fort, bis der Funktionswert des Berührpunktes (der Tangenten) möglichst nahe bei $0$ ist. Dann schneiden die Tangente und der nichtlineare Funktionsgraph die x-Achse nämlich an (fast) derselben Stelle.
Herleitung der Iterationsvorschrift
Schauen wir uns einmal, ausgehend von dem Startwert $x_0$, die Bestimmung von $x_1$ an.
Aufstellen der Tangentengleichung
Allgemein hat eine Tangentengleichung die Form $t(x)=m\cdot x+n$.
- Dabei ist $m=f'(x_0)$ die Steigung des Tangenten (die erste Ableitung von $f(x)$ an der Stelle $x_0$).
- $n$ ist der y-Achsenabschnitt. Dieser muss noch bestimmt werden.
Da der Punkt $P(x_0|f(x_0))$ auf der Tangente liegt, erhältst du diese Gleichung:
$f(x_0)=f'(x_0)\cdot x_0+n$.
Diese Gleichung kann nach $n$ umgeformt werden: $n=f(x_0)-f'(x_0)\cdot x_0$. Dies führt zu dieser Tangentengleichung:
$t(x)=f'(x_0)\cdot x+f(x_0)-f'(x_0)\cdot x_0$.
Bestimmung der Nullstelle der Tangente
Wir benennen nun die Nullstelle der Tangenten mit $x_1$, dann gilt $t(x_1)=0$ oder
$f'(x_0)\cdot x_1+f(x_0)-f'(x_0)\cdot x_0=0$ .
Division durch $f'(x_0)$ führt zu $x_1+\frac{f(x_0)}{f'(x_0)}-x_0=0$. Nun kann $x_0$ addiert und $\frac{f(x_0)}{f'(x_0)}$ subtrahiert werden:
$x_1=x_0-\frac{f(x_0)}{f'(x_0)}$.
Wenn du nun in dieser Gleichung auf der rechten Seite überall $x_0$ durch $x_1$ ersetzt, erhältst du $x_2$ und so weiter.
Die Iterationsvorschrift des Newton-Verfahrens
Damit kannst du die Iterationsvorschrift des Newton-Verfahrens angeben:
$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$.
Warum heißt das eigentlich „Iterationsvorschrift“?
Wenn du mit $x_0$ startest, kannst du $x_1$ berechnen. Mit diesem $x_1$ kannst du $x_2$ berechnen und damit $x_3$ und so weiter. Du kommst also Schritt für Schritt zu einer näherungsweisen Nullstelle, indem du die immer gleiche Vorschrift wiederholst.
„Iterare“ ist das lateinische Wort für „wiederholen“.
Beispiel
Nun üben wir das Newton-Verfahren einmal an einem Beispiel. Gesucht wird die Nullstelle dieser Funktion:
$f(x)=x^3-1,5x^2+x-1,5$.
Die zugehörige Ableitung ist $f'(x)=3x^2-3x+1$.
Der Startwert sei $x_0=2$. Der erste Schritt sieht dann so aus:
$x_1=2-\frac{f(2)}{f'(2)}=2-\frac{2,5}{7}\approx1,6429$.
Nun wird der Funktionswert $f(x_1)\approx 0,5286$ berechnet. Dies ist noch nicht so nahe bei $0$. Weiter geht's:
$x_2=1,6429-\frac{f(1,6429)}{f'(1,6429)}=1,6429-\frac{0,5286}{4,1687}\approx1,5161$.
Wieder wird der Funktionswert berechnet: $f(1,5161)\approx0,0531$. Du siehst, dass dieser Wert schon näher bei $0$ ist als der vorherige Funktionswert. Wir berechnen nun $x_3$:
$x_3=1,5161-\frac{f(1,5161)}{f'(1,5161)}=1,5161-\frac{0,0531}{3,3474}\approx1,5002$ .
Der Funktionswert an dieser Stelle ist $f(1,5002)\approx0,00045$. Dieser Wert ist schon sehr nahe bei $0$. Die tatsächlich Nullstelle liegt bei $x_N=1,5$.
Die Grenzen des Newton-Verfahrens
Die Funktion besitzt keine Nullstelle
Das Newton-Verfahren muss nicht unbedingt zu einer Lösung führen. Dies ist ganz sicher der Fall, wenn die Funktion gar keine Nullstelle besitzt.
Die Stellen wiederholen sich
Allerdings kann das Newton-Verfahren auch zu Stellen führen, welche immer wiederkehren. Dies kann man sich an einem Beispiel klarmachen: $f(x)=x^3-2x+2$ mit der Ableitung $f'(x)=3x^2-2$.
Sei nun $x_0=0$ der Startwert, dann erhältst du:
$x_1=0-\frac{f(0)}{f'(0)}=0-\frac{2}{-2}=1$.
Mit diesem $x_1$ kannst du ebenso $x_2$ berechnen:
$x_2=1-\frac{f(1)}{f'(1)}=1-\frac{1}{1}=1-1=0$.
Du siehst, dies ist die gleiche Stelle, mit welcher wir begonnen haben. Das bedeutet, dass $x_i=0$ gilt für jeden geraden Index $i$ und $1$ für jeden ungeraden Index $i$.
Die erste Ableitung ist 0
Schaue dir die Funktionsgleichung $f(x)=x^2-4$ an. Diese Funktion besitzt zwei Nullstellen bei $\pm 2$. Die Ableitung dieser Funktion ist $f'(x)=2x$.
Wenn nun der Startwert $x_0=0$ ist, folgt $f'(x_0)=0$. Das bedeutet, dass bei der Iterationsvorschrift
$x_1=x_0-\frac{f(x_0)}{f'(x_0)}$
durch $0$ dividiert wird. Dies ist natürlich verboten.
Worauf achtzugeben ist
Ganz allgemein kann man festhalten, dass die Konvergenz des Newton-Verfahrens mit der Wahl des Startwertes zusammenhängt. Es ist also wichtig, dass du eine ungefähre Vorstellung davon hast, wo die Nullstelle liegt, und entsprechend einen sinnvollen Startwert wählst.
Alle Videos zum Thema
Videos zum Thema
Extremwertaufgaben, Mittelwertsatz und Newton-Verfahren (9 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Extremwertaufgaben, Mittelwertsatz und Newton-Verfahren (9 Arbeitsblätter)
-
 Lösen von Extremwertaufgaben
PDF anzeigen
Lösen von Extremwertaufgaben
PDF anzeigen -
 Extremwertaufgabe – Schachtel
PDF anzeigen
Extremwertaufgabe – Schachtel
PDF anzeigen -
 Extremalprobleme – Anwendung der Differentialrechnung
PDF anzeigen
Extremalprobleme – Anwendung der Differentialrechnung
PDF anzeigen -
 Die Ziege – Extremwertaufgabe mit quadratischer Funktion
PDF anzeigen
Die Ziege – Extremwertaufgabe mit quadratischer Funktion
PDF anzeigen -
 Satz von Rolle
PDF anzeigen
Satz von Rolle
PDF anzeigen -
 Mittelwertsatz der Differentialrechnung
PDF anzeigen
Mittelwertsatz der Differentialrechnung
PDF anzeigen -
 Newton-Verfahren – Herleitung der Iterationsvorschrift
PDF anzeigen
Newton-Verfahren – Herleitung der Iterationsvorschrift
PDF anzeigen -
 Newton-Verfahren – Beispiel
PDF anzeigen
Newton-Verfahren – Beispiel
PDF anzeigen -
 Newton-Verfahren und seine Grenzen
PDF anzeigen
Newton-Verfahren und seine Grenzen
PDF anzeigen
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung




















