Stammfunktionen ganzrationaler Funktionen
Stammfunktionen tauchen vor allem in der Integralrechnung auf. Um das Integral einer Funktion zu berechnen, benötigt man immer die Stammfunktion. Deshalb lohnt es sich auch, Stammfunktionen einmal genauer zu betrachten.
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
Überblick
Betrachten wir $f(x)$ als eine beliebige integrierbare Funktion. Dann heißt jede Funktion $F(x)$, deren Ableitung $F'(x)=f(x)$ ist, Stammfunktion der Funktion $f(x)$.
Wenn $F(x)$ Stammfunktion von $f(x)$ ist, dann ist auch jede Funktion $F(x)+c$ mit $c \in \mathbb{R}$ eine Stammfunktion von $f(x)$. Konstanten fallen beim Ableiten nämlich weg:
$(F(x)+c)'=F'(x)+0=f(x)$.
Die Konstante $c$ wird als Integrationskonstante bezeichnet.
Die Menge aller Stammfunktionen wird als unbestimmtes Integral bezeichnet:
$\int~f(x)~dx = \{ F(x) | F'(x)=f(x) \}$
Ganzrationale Funktionen
In der Schule werden dir häufig ganzrationale Funktionen begegnen. Diese werden auch Polynome genannt und sehen wie folgt aus:
$f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+\dots +a_2x^2+a_1x+a_0$.
Es muss $a_n\neq 0$ gelten. Der Grad dieser Funktion ist der höchste Exponent $n$ und die Faktoren vor den Potenzen $a_n$, ..., $a_0$ werden als Koeffizienten der ganzrationalen Funktion bezeichnet.
Beispiele für ganzrationale Funktionen sind $f(x)=2x^4+x^2-2x+1$ oder $f(x)=\frac13 x^2+2x-3$.
Rechenregeln für unbestimmte Integrale
Wir wollen im Folgenden untersuchen, wie wir Stammfunktionen ganzrationaler Funktionen bestimmen können. Die Rechenregeln, die wir dazu benötigen, sind jeweils Umkehrungen von Rechenregeln der Differentiation: Potenzregel, Faktorregel und Summenregel.
Die Potenzregel der Integration
Wenn wir eine Potenzfunktion ableiten wollen, gilt $(x^n)'=n\cdot x^{n-1}$. Der Exponent wird als Faktor „nach vorne gezogen“ und verringert sich im Exponenten um $1$.
Beim Integrieren wird der Exponent umgekehrt um $1$ vergrößert. Zusätzlich wird durch den um $1$ erhöhten Exponenten dividiert:
$\int~x^n~dx=\frac1{n+1}\cdot x^{n+1}+c$.
Um nicht durch $0$ zu teilen, muss $n\neq -1$ gelten. Die Integrationskonstante $c$ muss nicht unbedingt berücksichtigt werden.
Schauen wir uns ein paar Beispiele an.
- $\int~x^3~dx=\frac1{3+1}\cdot x^{3+1}+c=\frac14x^4+c$
- $\int~x^6~dx=\frac17x^7+c$
- $\int~1~dx=\int~x^0~dx=\frac1{0+1}\cdot x^{0+1}+c=x+c$
Die Summenregel der Integration
Wenn wir eine Summe von Funktionen integrieren wollen, können wir jeden Summanden einzeln integrieren und die resultierenden Integrale dann addieren:
$\int~(u(x)+v(x))~dx=\int~u(x)~dx+\int~v(x)~dx$.
Schauen wir uns auch dazu ein paar Beispiele an.
- $\int~(x^3+x^2)~dx=\int~x^3~dx+\int~x^2~dx=\frac14x^4+\frac13x^3+c$
- $\int~(x^6-1)~dx=\int~x^6~dx-\int~1~dx=\frac17x^7-x+c$
Die Faktorregel der Integration
Wenn du das Produkt eines konstanten Faktors und einer Funktion integrieren sollst, integrierst du die Funktion und multiplizierst das resultierende Integral mit dem konstanten Faktor:
$\int~(k\cdot f(x))~dx=k\cdot \int~f(x)~dx$.
Das hört sich komplizierter an, als es in Wirklichkeit ist:
- $\int~(2x^3)~dx=2\cdot\int~x^3~dx=2\cdot \frac14x^4+c=\frac12x^4+c$,
- $\int~\left(\frac13x^6\right)~dx=\frac13\cdot\frac17x^7+c=\frac1{21}x^7+c$,
- $\int~k~dx=\int~(k\cdot 1)~dx= k \cdot \int~1~dx=kx+c$.
Wenn du überprüfen möchtest, ob die von dir ermittelte Stammfunktion korrekt ist, kannst du diese ableiten und das Ergebnis mit $f(x)$ vergleichen. Es gilt bekanntlich immer $F'(x)=f(x)$.
Bestimmte Integrale
Ein wichtiges Anwendungsgebiet der Integration ist die Flächenberechnung. Hierfür benötigen wir in der Regel das bestimmte Integral. Im Gegensatz zum unbestimmten Integral gibt es beim bestimmten Integral Integrationsgrenzen $a$ und $b$:
$\int\limits_a^b~f(x)~dx$.
Um das bestimmte Integral einer Funktion $f(x)$ in den Grenzen von $a$ bis $b$ zu berechnen, benötigst du zunächst eine Stammfunktion $F(x)$ von $f(x)$. Dann kannst du das bestimmte Integral mit dem Hauptsatz der Differential- und Integralrechnung berechnen.
Der Hauptsatz der Differential- und Integralrechnung
Mit dem Hauptsatz der Differential- und Integralrechnung gilt
$\int\limits_a^b~f(x)~dx=[F(x)]_a^b=F(b)-F(a)$.
Im Allgemeinen gibt das bestimmte Integral eine Flächenbilanz an. Wenn der Graph einer Funktion auf einem Intervall $I=[a;b]$ oberhalb oder auf der x-Achse liegt, gibt das bestimmte Integral einen Flächeninhalt an.
Beispiel
Schauen wir uns ein Beispiel an: $f(x)=x^3-3x^2+4$. Den zugehörigen Funktionsgraphen kannst du hier sehen:
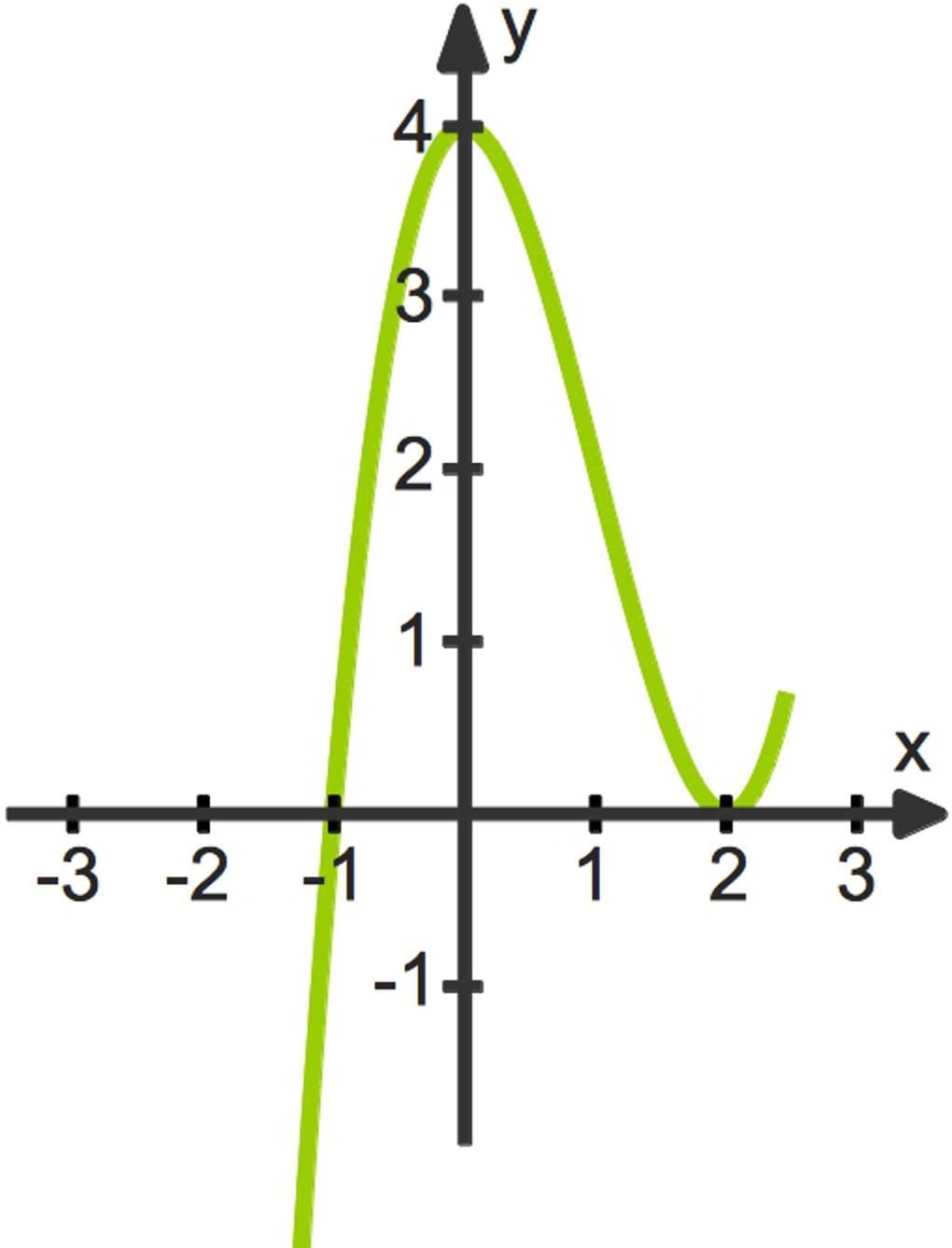
Wir wollen den Inhalt des Flächenstücks berechnen, welches von der x-Achse und dem Graphen der Funktion über dem Intervall $I=[0;2]$ eingeschlossen wird. Du kannst in dem Bild erkennen, dass der Funktionsgraph auf diesem Intervall komplett oberhalb oder auf der x-Achse liegt.
Die untere Integrationsgrenze ist $a=0$, die obere Integrationsgrenze ist $b=2$. Damit wird der gesuchte Flächeninhalt beschrieben durch:
$A=\int \limits_0^2~(x^3-3x^2+4)~dx$.
Im nächsten Schritt wollen wir die Stammfunktion $F(x)$ von $f(x)$ finden. In der Regel wird die Integrationskonstante bei der Ermittlung von Stammfunktionen vernachlässigt. Wir verwenden die uns bekannten Integrationsregeln (**Potenz-, Summen- sowie Faktorregel:
$F(x)=\frac14x^4-x^3+4x$.
Nun können wir endlich den Hauptsatz der Differential- und Integralrechnung anwenden:
$\begin{array}{rcl} A&=&\int\limits_0^2~(x^3-3x^2+4)~dx\\ &=&\left[\frac14x^4-x^3+4x\right]_0^2\\ &=&\left(\frac142^4-2^3+4\cdot 2\right)-\left(\frac140^4-0^3+4\cdot 0\right)\\ &=&4 \end{array}$
Das Flächenstück hat den Inhalt $4$ [FE].
Alle Videos und Lerntexte zum Thema
Videos und Lerntexte zum Thema
Stammfunktionen ganzrationaler Funktionen (6 Videos, 1 Lerntext)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Stammfunktionen ganzrationaler Funktionen (6 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung









 Stammfunktionen berechnen
Stammfunktionen berechnen
 Potenzregel für Integrale
Potenzregel für Integrale
 Faktor- und Summenregel für Integrale
Faktor- und Summenregel für Integrale
 Lineare Substitutionsregel für Integrale
Lineare Substitutionsregel für Integrale
 Integralfunktion – Definition
Integralfunktion – Definition
 Graphisches Aufleiten
Graphisches Aufleiten









