Satz des Thales
Der Satz des Thales besagt: Für jeden Punkt C, außer A und B, auf dem Halbkreis über der Strecke AB gilt, dass das Dreieck ΔABC rechtwinklig ist mit dem rechten Winkel in C
Jetzt mit Spass die Noten verbessern
und sofort Zugriff auf alle Inhalte erhalten!
30 Tage kostenlos testenInhaltsverzeichnis zum Thema
- Leuchttürme: Eine Anwendung des Satzes des Thales
- Der Satz des Thales
- Beweis des Satzes von Thales
- Konstruktion von Tangenten an einen Kreis
Leuchttürme: Eine Anwendung des Satzes des Thales

Von einem Segelschiff aus werden zwei Leuchttürme angepeilt. Sie sind unter einem Blickwinkel von $90^\circ$ zu sehen. Das Segelschiff bewegt sich nun so, dass die beiden Leuchttürme immer unter einem Blickwinkel von $90^\circ$ zu sehen sind. Wie sieht die Bahn aus, auf welcher sich das Segelschiff bewegt?
Schauen wir uns das mal in einer Skizze an.
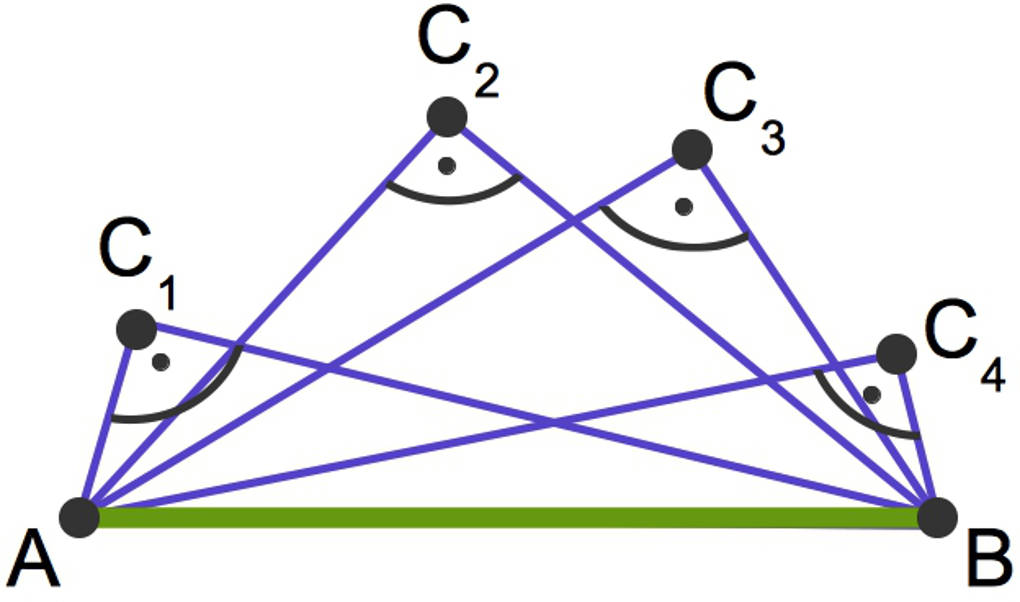
Die beiden Leuchttürme seien die Punkte $A$ und $B$. Die verschiedenen Positionen des Segelschiffes werden mit $C_1$, $C_2$, $C_3$ und $C_4$ bezeichnet. Jedes der so erhaltenen Dreiecke mit den Eckpunkten $A$ und $B$ sowie der jeweiligen Position des Segelschiffes ist rechtwinklig:
- Der rechte Winkel befindet sich in dem Punkt, der die Position des Segelschiffes beschreibt.
- Die Strecke $\overline{AB}$ ist die Hypotenuse dieses Dreiecks. Die beiden anderen Seiten, die Abstände des Segelschiffes zu den Leuchttürmen, sind die Katheten.
Fällt dir etwas auf, wenn du dir die verschiedenen Eckpunkte $C_1$, $C_2$, $C_3$ und $C_4$ anschaust?
Alle diese Punkte liegen auf einem Halbkreis. Der Durchmesser dieses Halbkreises ist die Strecke $\overline{AB}$.
Das bedeutet, dass das Segelschiff sich auf einem Halbkreis bewegt.
Der Satz des Thales
Der Satz des Thales besagt: Für jeden Punkt $C$, außer $A$ und $B$, auf dem Halbkreis über der Strecke $\overline{AB}$ gilt, dass das Dreieck $\Delta_{ABC}$ rechtwinklig ist mit dem rechten Winkel in $C$.

Natürlich gilt dieser Satz auch für den gespiegelten Halbkreis, also für den gesamten Kreis.
Dieser Satz wurde von Thales von Milet (6. Jh v. Chr) einem griechischen Mathematiker, bewiesen.
Es gilt auch die Umkehrung dieses Satzes: Sei das Dreieck $\Delta_{ABC}$ rechtwinklig mit dem rechten Winkel in $C$, dann liegt der Punkt $C$ auf einem Halbkreis über der Strecke $\overline{AB}$. Das bedeutet, dass der Umkreis des Dreiecks den Durchmesser $\overline{AB}$ besitzt. Also ist der Mittelpunkt des Umkreises der Mittelpunkt der Hypotenuse.
Der Halbkreis wird auch als Thales-Kreis bezeichnet.
Beweis des Satzes von Thales
Um den Satz des Thales zu beweisen, wird der Mittelpunkt $D$ des Thaleskreises mit dem Punkt $C$ verbunden.
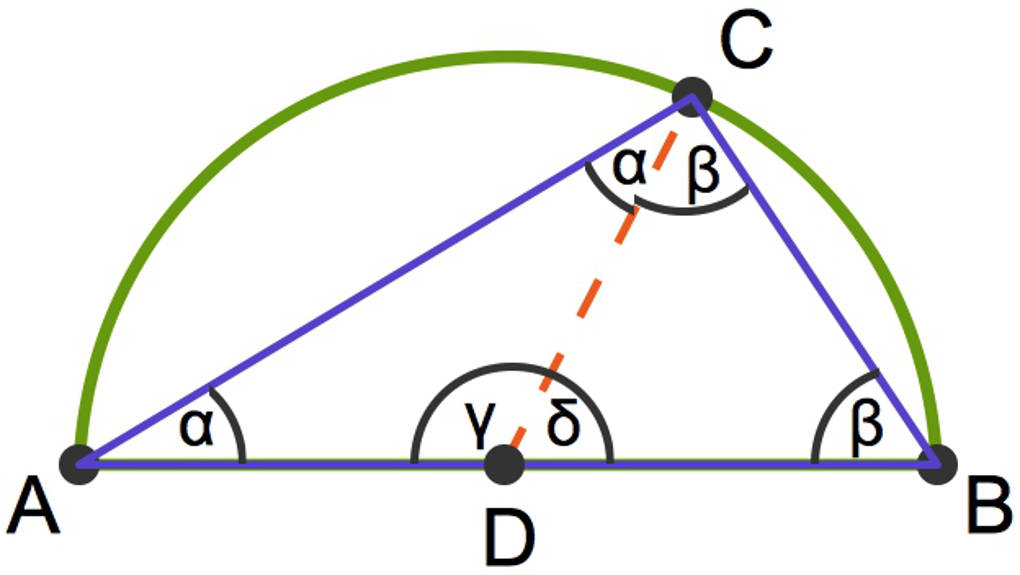
So entstehen zwei gleichschenklige Dreiecke $\Delta_{ADC}$ sowie $\Delta_{DBC}$. Die jeweiligen Basiswinkel ($\alpha$ beziehungsweise $\beta$) sind gleich groß. Nach dem Winkelsummensatz in Dreiecken gilt, dass die Summe der Innenwinkel eines beliebigen Dreiecks immer $180^\circ$ beträgt. Es gilt also
- $2\alpha+\gamma=180^\circ$ und ebenso
- $2\beta+\delta=180^\circ$.
Du erhältst durch Addition $2\alpha+\gamma+2\beta+\delta=360^\circ$. Da $\gamma+\delta=180^\circ$ ist, kannst Du $180^\circ$ auf beiden Seiten subtrahieren. Zusätzlich kannst du $2$ ausklammern. Dies führt zu $2(\alpha+\beta)=180^\circ$. Division durch $2$ ergibt $\alpha+\beta=90^\circ$. Dies ist der Winkel bei $C$.
Konstruktion von Tangenten an einen Kreis
Du sollst das folgende Problem lösen: Gegeben ist ein Kreis mit dem Mittelpunkt $M$ sowie ein Punkt $P$ außerhalb des Kreises. Wie kannst Du die beiden (!) Geraden zeichnen, auf denen der Punkt $P$ liegt und die den Kreis berühren? Diese Geraden werden als Tangenten bezeichnet.
Sei $B_1$ ein Berührpunkt, dann gilt, dass $\overline{MB_1}$ mit der entsprechenden Geraden einen Winkel der Größe $90^\circ$ einschließt. Wie kannst Du nun einen solchen Punkt finden? Hierfür verwendest Du den Satz des Thales:
- Du zeichnest einen Halbkreis über der Strecke $\overline{PM}$.
- Dort, wo dieser Halbkreis den Kreis mit dem Mittelpunkt $M$ schneidet, befindet (befinden) sich der (die) gesuchte(n) Berührpunkt(e).
Dies kannst du hier sehen:
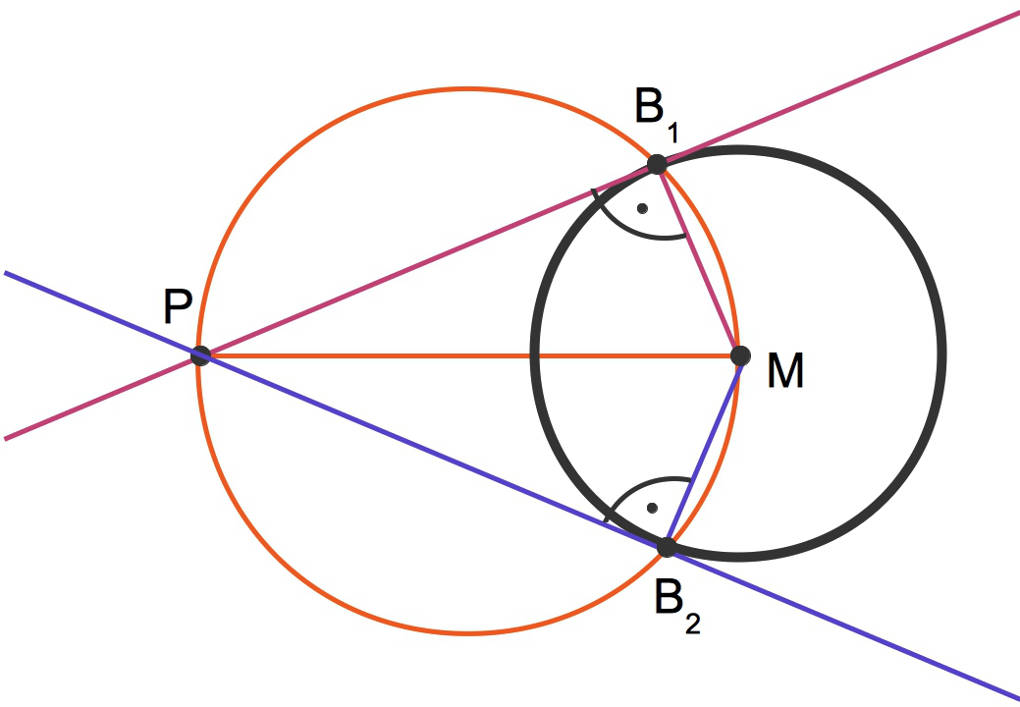
Verbinde nun $P$ mit dem Berührpunkt $B_1$, so erhältst du die violette Tangente und mit $B_2$, so erhältst du die blaue Tangente.
Alle Videos zum Thema
Videos zum Thema
Satz des Thales (2 Videos)
Alle Arbeitsblätter zum Thema
Arbeitsblätter zum Thema
Satz des Thales (2 Arbeitsblätter)
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 Satz des Thales
Satz des Thales
 Satz des Thales – Anwendung
Satz des Thales – Anwendung









