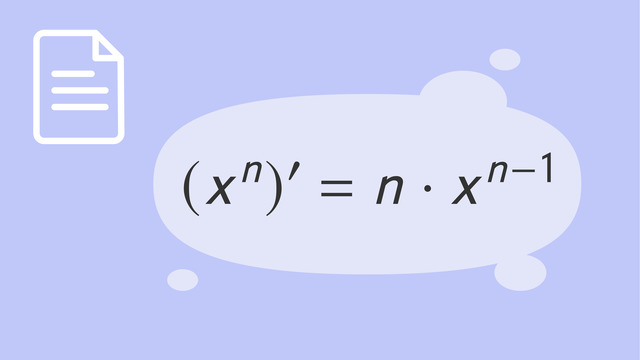Potenzregel bei Ableitungen – Beweis
Die Potenzregel hilft dir, die Ableitung einer Potenzfunktion zu bestimmen. Mit der vollständigen Induktion kannst du den Beweis nachvollziehen. Interessiert? Lies weiter und entdecke die Details!
- Potenzregel bei Ableitungen – benötigtes Vorwissen
- Die Potenzregel
- Induktionsbeweis der Potenzregel – Induktionsanfang
- Induktionsbeweis der Potenzregel – Induktionsvoraussetzung
- Induktionsbeweis der Potenzregel – Induktionsschritt
- Induktionsbeweis der Potenzregel – Induktionsschluss
in nur 12 Minuten? Du willst ganz einfach ein neues
Thema lernen in nur 12 Minuten?
-
 5 Minuten verstehen
5 Minuten verstehen
Unsere Videos erklären Ihrem Kind Themen anschaulich und verständlich.
92%der Schüler*innen hilft sofatutor beim selbstständigen Lernen. -
 5 Minuten üben
5 Minuten üben
Mit Übungen und Lernspielen festigt Ihr Kind das neue Wissen spielerisch.
93%der Schüler*innen haben ihre Noten in mindestens einem Fach verbessert. -
 2 Minuten Fragen stellen
2 Minuten Fragen stellen
Hat Ihr Kind Fragen, kann es diese im Chat oder in der Fragenbox stellen.
94%der Schüler*innen hilft sofatutor beim Verstehen von Unterrichtsinhalten.
Lerntext zum Thema Potenzregel bei Ableitungen – Beweis
Potenzregel bei Ableitungen – benötigtes Vorwissen
Für dieses Thema solltest du wissen, was eine Potenzfunktion ist und wie man sie mit der Potenzregel ableitet. Zur Erinnerung:
Eine Potenzfunktion sieht im Allgemeinen so aus:
$f(x) = x^{n}$ für $n \in \mathbb{N}\setminus{{0}}$
Weiterhin solltest du die Vorgehensweise der vollständigen Induktion zum Beweisen von mathematischen Aussagen kennen. Zusammengefasst funktioniert diese so:
Die vollständige Induktion ist eine Beweismethode für mathematische Aussagen, die alle natürlichen Zahlen umfassen. In Kurzform kann eine solche Aussage mit $A$ abgekürzt werden. $A(n)$ verdeutlicht dann, dass diese Aussage für alle natürlichen Zahlen $n$ gelten soll. Man zeigt die Aussage für eine kleinste Zahl ($n=1$). Das ist der Induktionsanfang. Dann zeigt man, dass, wenn die Aussage für eine beliebige Zahl $k$ gilt, sie auch für die Nachfolgerzahl $k + 1$ gilt (Induktionsschritt). In Kombination beweist das dann, dass die Aussage für alle natürlichen Zahlen gilt.
Die Potenzregel
Die Potenzregel bei Ableitungen lautet für $n \in \mathbb{N}$:
$(x^{n})^{\prime} = n \cdot x^{n-1}$
Diese wollen wir im Folgenden mit der vollständigen Induktion beweisen.
Induktionsbeweis der Potenzregel – Induktionsanfang
Dazu schauen wir uns zunächst den Induktionsanfang $n = 1$ an:
$\begin{array}{rcccl} \text{Induktionsanfang (I. A.):} & n = 1 & \\ & \implies & (x^{1})^{\prime} & = & 1 \cdot x^{1-1} \\ & \Leftrightarrow & (x)^{\prime} & = & 1 \cdot x^{0} \\ & \Leftrightarrow & (x)^{\prime} & = & 1 \\ \end{array}$
Dass $x$ abgeleitet tatsächlich $1$ ergibt, können wir mit dem Differenzialquotienten zeigen. Zur Erinnerung:
Mit dem Differenzialquotienten können wir die Ableitung einer Funktion $f(x)$ an der Stelle $x_{0}$ berechnen. Das sieht so aus:
$f^{\prime}(x_{0}) = \lim\limits_{x \to x_{0}} \dfrac{f(x)~–~f(x_{0})}{x~–~x_{0}}$
In diesem Fall haben wir $f(x) = x$. Also haben wir mit dem Differenzialquotienten:
$f^{\prime}(x_{0}) = \lim\limits_{x \to x_{0}} \dfrac{x~–~x_{0}}{x~–~x_{0}} = 1$
Damit gilt also:
$\begin{array}{rcccl} \text{Induktionsanfang (I. A.):} & n = 1 & \\ & \Leftrightarrow & (x)^{\prime} & = & 1 \\ & \Leftrightarrow & 1 & = & 1 \\ \end{array}$
Der I. A. ist damit korrekt und wir können mit der Induktionsvoraussetzung (I. V.) weitermachen.
Induktionsbeweis der Potenzregel – Induktionsvoraussetzung
Aufgrund der Gültigkeit des I. A. können wir nun die Induktionsvoraussetzung (I. V.) aufstellen:
Induktionsvoraussetzung (I. V.): $A(n)$ gilt für ein $n \in \mathbb{N}$.
Dies sagt zunächst nur, dass die Aussage, die wir beweisen wollen, für ein bestimmtes $n$ gilt. Um zu beweisen, dass sie auch für alle $n \in \mathbb{N}$ gilt, müssen wir als Nächstes den Induktionsschritt (I. S.) gehen.
Induktionsbeweis der Potenzregel – Induktionsschritt
Für den Induktionsschritt (I. S.) nehmen wir die Induktionsvoraussetzung (I. V.) und beweisen, dass die Aussage auch für die entsprechende Nachfolgerzahl $n + 1$ gilt.
$\begin{array}{lccl} \text{Induktionsschritt (I. S.):} & n \rightarrow n + 1 & & \\ \\ \quad & (x^{n})^{\prime} & = & n \cdot x^{n~–~1} \\ \\ \quad \Rightarrow & (x^{n + 1})^{\prime} & = & (n + 1) \cdot x^{n} \\ \end{array}$
Dies werden wir im Folgenden beweisen. Zunächst nutzen wir ein Potenzgesetz zur Multiplikation von Potenzen mit gleicher Basis, um den betrachteten Term umzuformen.
$\begin{array}{lccl} \text{Induktionsschritt (I. S.):} & n \rightarrow n + 1 & & \\ \\ \quad & (x^{n + 1})^{\prime} & = & (x \cdot x^{n})^{\prime} \\ \end{array}$
Nun können wir die Produktregel für Ableitungen anwenden. Kurz zur Erinnerung:
Die Produktregel für Ableitungen besagt:
$(u(x) \cdot v(x))^{\prime} = u^{\prime}(x) \cdot v(x) + u(x) \cdot v^{\prime}(x)$
In diesem Fall gilt:
$u(x) = x \quad u^{\prime}(x) = 1 \quad v(x) = x^{n} \quad v^{\prime}(x) = (x^{n})^{\prime}$
Damit können wir also weiter umformen:
$\begin{array}{lccl} \text{I. S:} & n \rightarrow n + 1 & & \\ \\ \quad & (x^{n + 1})^{\prime} & = & (x \cdot x^{n})^{\prime} \\ \\ & & = & 1 \cdot x^{n} + x \cdot (x^{n})^{\prime} = x^{n} + x \cdot (x^{n})^{\prime} \\ \end{array}$
Nun ist es an der Zeit, den Trick der vollständigen Induktion als Methode anzuwenden. Dadurch dass wir als Voraussetzung gesetzt haben, dass die Aussage, die wir beweisen wollen (also die Potenzregel für Ableitungen) für ein beliebiges $k$ gilt, können wir dies hier anwenden. Die Voraussetzung lautete:
$\text{I. V:} ~~(x^{n})^{\prime} = n \cdot x^{n~–~1}$
Diese Gleichung können wir im Induktionsbeweis nun nutzen, um $(x^{n})^{\prime}$ zu ersetzen:
$\begin{array}{lccl} \text{I. S:} & n \rightarrow n + 1 & & \\ \\ \quad & (x^{n + 1})^{\prime} & = & (x \cdot x^{n})^{\prime} \\ \\ & & = & 1 \cdot x^{n} + x \cdot (x^{n})^{\prime} = x^{n} + x \cdot (x^{n})^{\prime} \\ \\ & & = & x^{n} + x \cdot n \cdot x^{n~–~1} = x^{n} + n \cdot x^{1} \cdot x^{n~–~1} \\ \\ & & = & x^{n} + n \cdot x^{n} = (n + 1) \cdot x^{n} \\ \end{array}$
Wir sind am Ende unserer Umformungen angekommen und haben das gezeigt, was wir zeigen wollten: $(x^{n + 1})^{\prime}= (n + 1) \cdot x^{n}$
Zum Abschluss formulieren wir noch den Induktionsschluss.
Induktionsbeweis der Potenzregel – Induktionsschluss
Aufgrund unserer Ergebnisse im I. S. können wir nun den Induktionsschluss beschreiben:
Induktionsschluss: $A(n)$ gilt für alle $n \in \mathbb{N}$.
Damit ist die vollständige Induktion abgeschlossen und die Potenzregel bewiesen.
Induktionsbeweis der Potenzregel bei Ableitungen – Zusammenfassung
Dadurch dass die Potenzregel bei Ableitungen auf natürlichen Zahlen im Exponenten basiert, kann sie mithilfe der Methode der vollständigen Induktion bewiesen werden. Dazu wird die Potenzregel für ein beliebiges $n + 1$ bewiesen, indem vorausgesetzt wird, dass sie für ein beliebiges $n$ gilt. Die Methode der vollständigen Induktion sieht dabei so aus:
| Induktionsanfang (I. A.): | Beweis der Aussage $A(n)$ für $n = a$ mit $a$ als kleinster Zahl (in der Regel ist $a = 1$) |
|---|---|
| Induktionsvoraussetzung (I. V.): | $A(n)$ gilt für ein $n \in \mathbb{N}$. |
| Induktionsschritt (I. S.): | $A(n)$ gilt, also wird damit bewiesen, dass auch $A(n + 1)$ gilt. |
| Induktionsschluss: | $A(n)$ gilt für alle $n \in \mathbb{N}$. |
Häufig gestellte Fragen zum Thema Induktionsbeweis der Potenzregel
9'802
sofaheld-Level
6'600
vorgefertigte
Vokabeln
7'802
Lernvideos
37'205
Übungen
32'636
Arbeitsblätter
24h
Hilfe von Lehrkräften

Inhalte für alle Fächer und Schulstufen.
Von Expert*innen erstellt und angepasst an die Lehrpläne der Bundesländer.
Testphase jederzeit online beenden
Beliebteste Themen in Mathematik
- Römische Zahlen
- Prozentrechnung
- Prozentrechnung - Übungen
- Primzahlen
- Geometrische Lagebezeichnungen
- Was ist eine Ecke?
- Rechteck
- Was ist eine Gleichung?
- Pq-Formel
- Satz des Pythagoras – Übungen
- Binomische Formeln
- Graphisches Ableiten – Übungen
- Trapez
- Flächeninhalt – Übungen
- Volumen Zylinder
- Potenzgesetze – Übungen
- Umfang Kreis
- Zehnerzahlen vergleichen und ordnen – Übungen
- Quadrat
- Zahlen sortieren – Übungen
- Division
- Binomische Formeln – Übungen
- Raute
- Brüche umwandeln Übungen
- Parallelogramm
- Ungleichungen – Übungen
- Polynomdivision
- Zahlen bis 1000 ordnen – Übungen
- Was Ist Eine Viertelstunde
- Terme mit Variablen aufstellen – Übungen
- Prisma
- Die Grundrechenarten – Übungen
- Mitternachtsformel
- Äquivalenzumformung
- Grundrechenarten Begriffe
- Größer Kleiner Zeichen
- Dreiecksarten
- Punkt-vor-Strich und Klammern-zuerst-Regel
- Aufbau von Dreiecken
- Quader
- Zahlen runden – Übungen
- Satz Des Pythagoras
- Ziffern und Stellenwerte – Übungen
- Dreieck Grundschule
- Koordinatensystem – Übungen
- Erste Binomische Formel
- Kreis
- Trigonometrie
- Trigonometrische Funktionen
- Standardabweichung


 5 Minuten verstehen
5 Minuten verstehen
 5 Minuten üben
5 Minuten üben
 2 Minuten Fragen stellen
2 Minuten Fragen stellen

 Bereit für eine echte Prüfung?
Bereit für eine echte Prüfung?