Grundlagen zur Kurvendiskussion

Inhaltsverzeichnis zum Thema

• Überblick
• Der Definitionsbereich und der Wertebereich einer Funktion
  • Der Definitionsbereich
  • Der Wertebereich
• Symmetrie einer Funktion
• Die Nullstellen einer Funktion
• Die Extrema einer Funktion
  • Notwendige und hinreichende Bedingung für Extrema
  • Monotonie
  • Vorzeichenwechselkriterium
• Die Wendepunkte einer Funktion
• Der Graph einer Funktion

Überblick

Hier kannst du die einzelnen Schritte einer Kurvendiskussion ganz rationaler Funktionen im Überblick sehen.

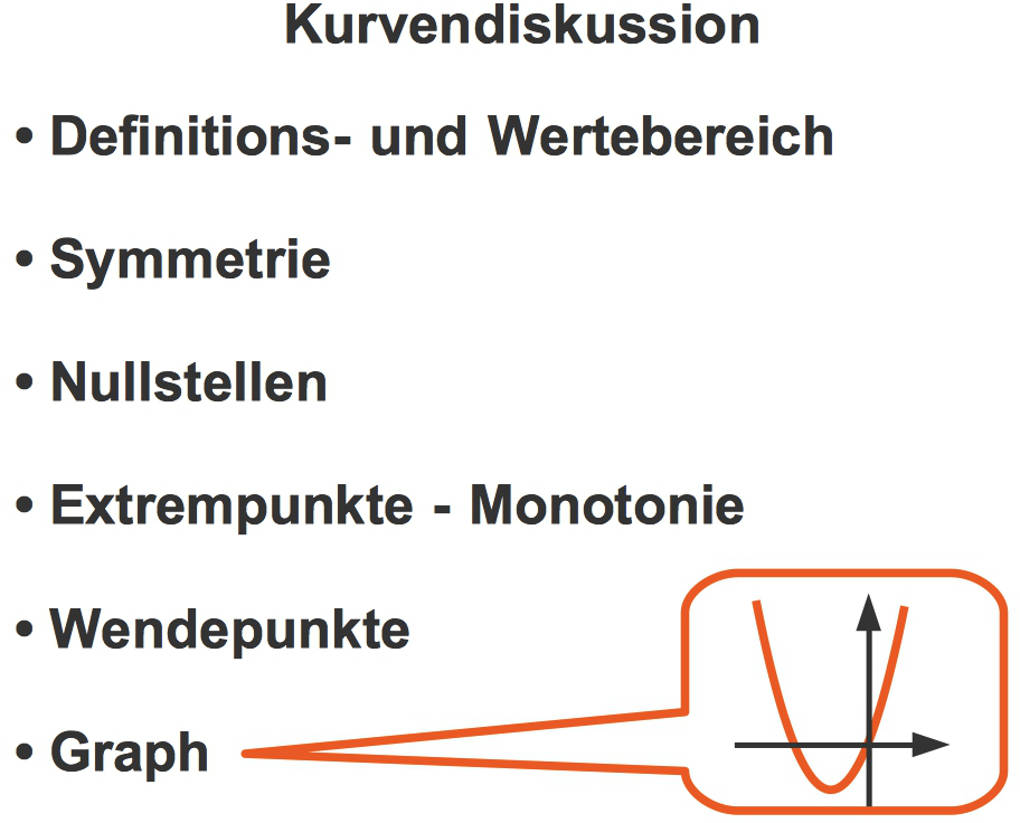
Um dieses Vorgehen genauer zu verstehen, wollen wir uns eine kubischen Funktion etwas näher ansehen. Die Funktionsgleichung ist diese:

$f(x)=x^3-3x^2+4$.

Der Definitionsbereich und der Wertebereich einer Funktion

Der Definitionsbereich

Der Definitionsbereich, oder auch die Definitionsmenge, $\mathbb{D}_f$ einer Funktion ist die Menge aller Werte, welche für das Argument $x$ in die Funktionsvorschrift eingesetzt werden können, sodass die Funktion definiert ist.

Dies können wir besser verstehen, wenn wir uns Funktionen ansehen, welche nicht für alle reellen Zahlen definiert sind:

• Die Wurzelfunktion $g(x)=\sqrt{x}$ ist nur für positive reelle Zahlen und die $0$ definiert. Man schreibt dies so: $\mathbb{D}_g=\mathbb{R}^+_0$.
• Die Hyperbelfunktion $h(x)=\frac1x$ ist nicht für $x=0$ definiert, also $\mathbb{D}_h=\mathbb{R}\setminus\{0\}$. Die $0$ wird also aus dem Definitionsbereich ausgeschlossen. Man bezeichnet sie deshalb als Definitionslücke.

Ganzrationale Funktionen sind für alle reellen Zahlen definiert. Somit ist auch unsere kubische Funktion f(x)=x³-3x²+4 für alle reellen Zahlen definiert: $\mathbb{D}_f=\mathbb{R}$.

Der Wertebereich

Der Wertebereich $\mathbb{W}_f$ einer Funktion ist die Menge aller Werte, welche die Funktion annimmt. Hierfür kannst du dir die Extrema sowie die Grenzwerte einer Funktion anschauen. Schauen wir uns ein paar Beispiele für Wertebereiche an:

• $g(x)=\sqrt{x}$ hat den Wertebereich $\mathbb{W}_g=\mathbb{R}^+_0$.
• $h(x)=\frac1x$ hat den Wertebereich $\mathbb{W}_h=\mathbb{R}\setminus\{0\}$.
• $f(x)=x^3-3x^2+4$ hat den Wertebereich $\mathbb{W}_f=\mathbb{R}$.

Symmetrie einer Funktion

Ganz allgemein wird die Symmetrie einer Funktion wie folgt überprüft:

• Ist $f(-x)=f(x)$ für alle $x\in\mathbb{D}_f$, dann ist die Funktion achsensymmetrisch zur y-Achse oder auch gerade symmetrisch.
• Ist $f(-x)=-f(x)$ für alle $x\in\mathbb{D}_f$, dann ist die Funktion punktsymmetrisch zum Koordinatenursprung oder auch ungerade symmetrisch.
• Ansonsten liegt keine der beiden Symmetrien vor.

Bei ganzrationalen Funktionen kannst du die Symmetrie direkt an den Exponenten erkennen. Dies erklärt auch den Namen der geraden oder ungeraden Symmetrie.

• Sind bei einer ganzrationalen Funktion alle Exponenten gerade, dann ist die Funktion achsensymmetrisch zur y-Achse.
• Sind bei einer ganzrationalen Funktion alle Exponenten ungerade, dann ist die Funktion punktsymmetrisch zum Koordinatenursprung.

$f(x)=x^3-3x^2+4$ hat sowohl gerade als auch ungerade Exponenten. Es liegt also keine der obigen Symmetrien vor.

Die Nullstellen einer Funktion

Die Nullstellen einer Funktion $f(x)$ sind alle Werte $x$ einer Funktion, für die $f(x)=0$ gilt. Das bedeutet, wenn du eine Nullstelle für $x$ in die Funktionsgleichung einsetzt, erhältst du den Funktionswert $y=f(x)=0$. Beachte dabei, dass sich der Begriff „Nullstelle“ ausschließlich auf die $x$-Koordinate bezieht.

Schauen wir uns das Beispiel $f(x)=x^3-3x^2+4$ an:

• Die erste Nullstelle muss geraten werden, weil wir hier keines der üblichen Verfahren anwenden können.
• Eine Nullstelle liegt aber bei $x_1=2$, denn $f(2)=2^3-3\cdot 2^2+4=8-12+4=0$.
• Nun kannst du die weiteren Nullstellen mit Hilfe der Polynomdivision sowie der p-q-Formel erhalten.
• Die weiteren Nullstellen sind $x_2=-1$ und $x_3=2$.
• Du siehst schon, dass $x_1=x_3=2$ eine doppelte Nullstelle ist. Was dies bedeutet, erfährst du bei den Extrema.

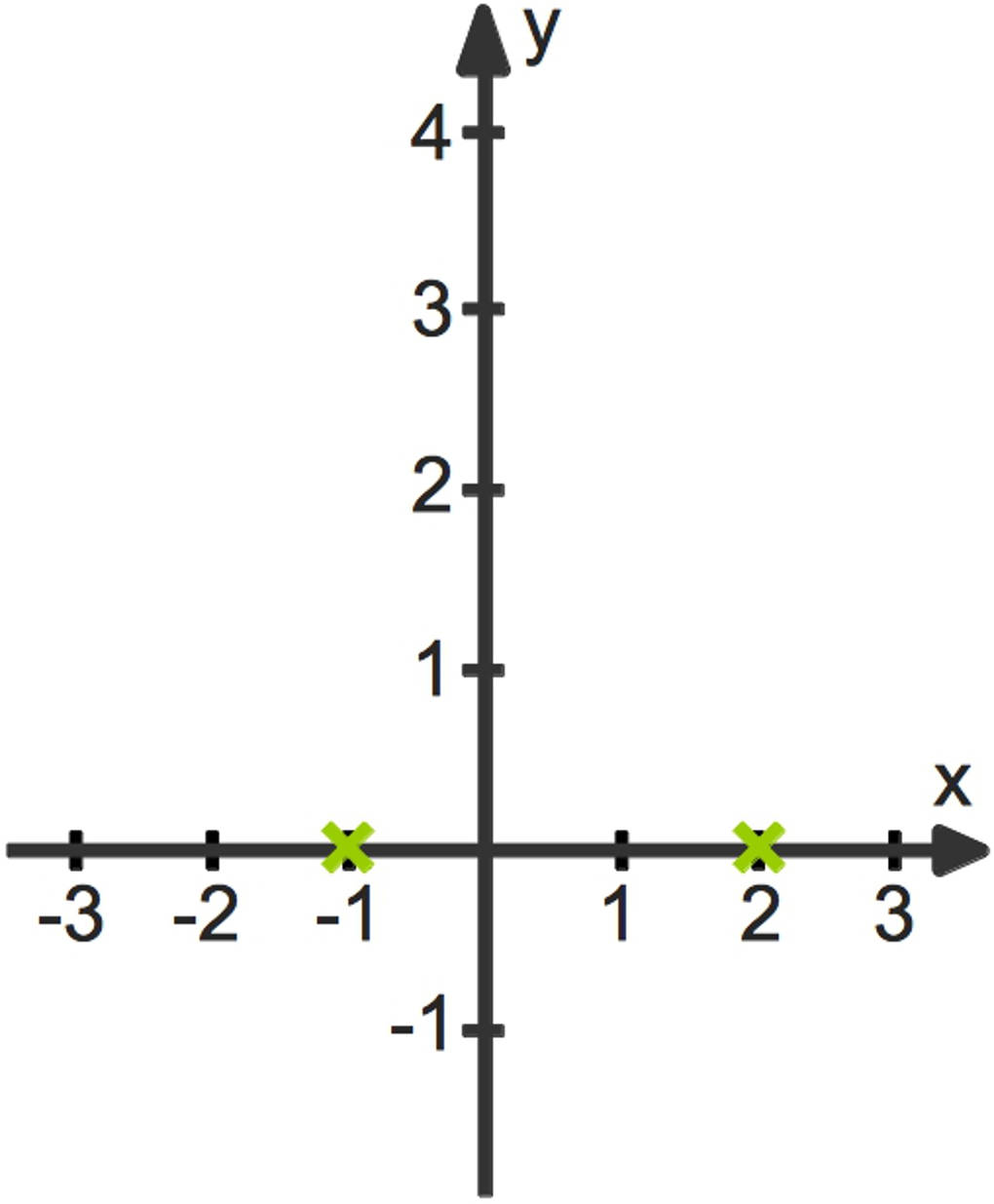
Tipp: Zeichne deine Ergebnisse fortlaufend in ein Koordinatensystem. Hier sind bereits die Nullstellen eingetragen.

Die Extrema einer Funktion

Die Extremstelle einer Funktion ist die Stelle, an welcher der Funktionswert größer (oder kleiner) ist als die anderen Funktionswerte in der Umgebung dieser Stelle. Deshalb spricht man auch von einem lokalen Extremum. Liegt der absolut höchste oder niedrigste Funktionswert vor, spricht man von einem globalen Extremum.

Hochpunkte werden auch als Maxima bezeichnet, Tiefpunke heißen auch Minima.

Zur Bestimmung der Extrema einer Funktion kannst du entweder

• die notwendige und hinreichende Bedingung mit der ersten und zweiten Ableitung überprüfen oder
• die erste Ableitung auf einen Vorzeichenwechsel untersuchen.

In jedem Fall benötigen wir die erste Ableitung der Funktion $f(x)=x^3-3x^2+4$. Diese erhältst du mit der Potenzregel, der Faktorregel sowie der Summenregel der Differentiation:

$f'(x)=3x^2-6x$.

Notwendige und hinreichende Bedingung für Extrema

Hierfür benötigst du noch die zweite Ableitung

$f''(x)=6x-6$.

Die notwendige Bedingung für Extrema besagt, dass die erste Ableitung an einer Extremstelle $0$ sein muss, also $f'(x_E)=0$. Dies bedeutet anschaulich, dass an dieser Stelle eine waagerechte Tangente vorliegt. Hier musst du also eine Gleichung lösen:

$\begin{array}{ccclll} &f'(x)&=&0\\ \Leftrightarrow&3x^2-6x&=&0&|&\text{Ausklammern}\\ \Leftrightarrow&3x(x-2)&=&0\\ \Rightarrow&x_{E_1}&=&0\\ &x_{E_2}&=&2 \end{array}$

Nun ist jedoch nicht jede Stelle mit waagerechter Tangente auch eine Extremstelle. Du musst zusätzlich die hinreichende Bedingung $f''(x_E)\neq0$ überprüfen. Das Vorzeichen gibt dann an, welcher Art das Extremum ist. Untersuchen wir die beiden ermittelten Stellen:

$f''(0)=6 \cdot 0-6=-6<0$.

Da die zweite Ableitung negativ ist, liegt hier ein (lokaler) Hochpunkt vor. Dieser ist $HP(0|4)$. Die y-Koordinate erhältst du durch Einsetzen von $x_{E_1}=0$ in die Funktionsvorschrift: $y=f(0)=0^3-3\cdot 0^2+4=4$.

Untersuchen wir noch die zweite Stelle:

$f''(2)=6\cdot 2-6=6>0$.

Die zweite Ableitung ist positiv. Es liegt ein (lokaler) Tiefpunkt vor. Dieser ist $TP(2|0)$.

Übrigens liegt bei $x_{E_2}=x_1=x_3=2$ ein doppelte Nullstelle vor. Eine solche ist immer eine Extremstelle.

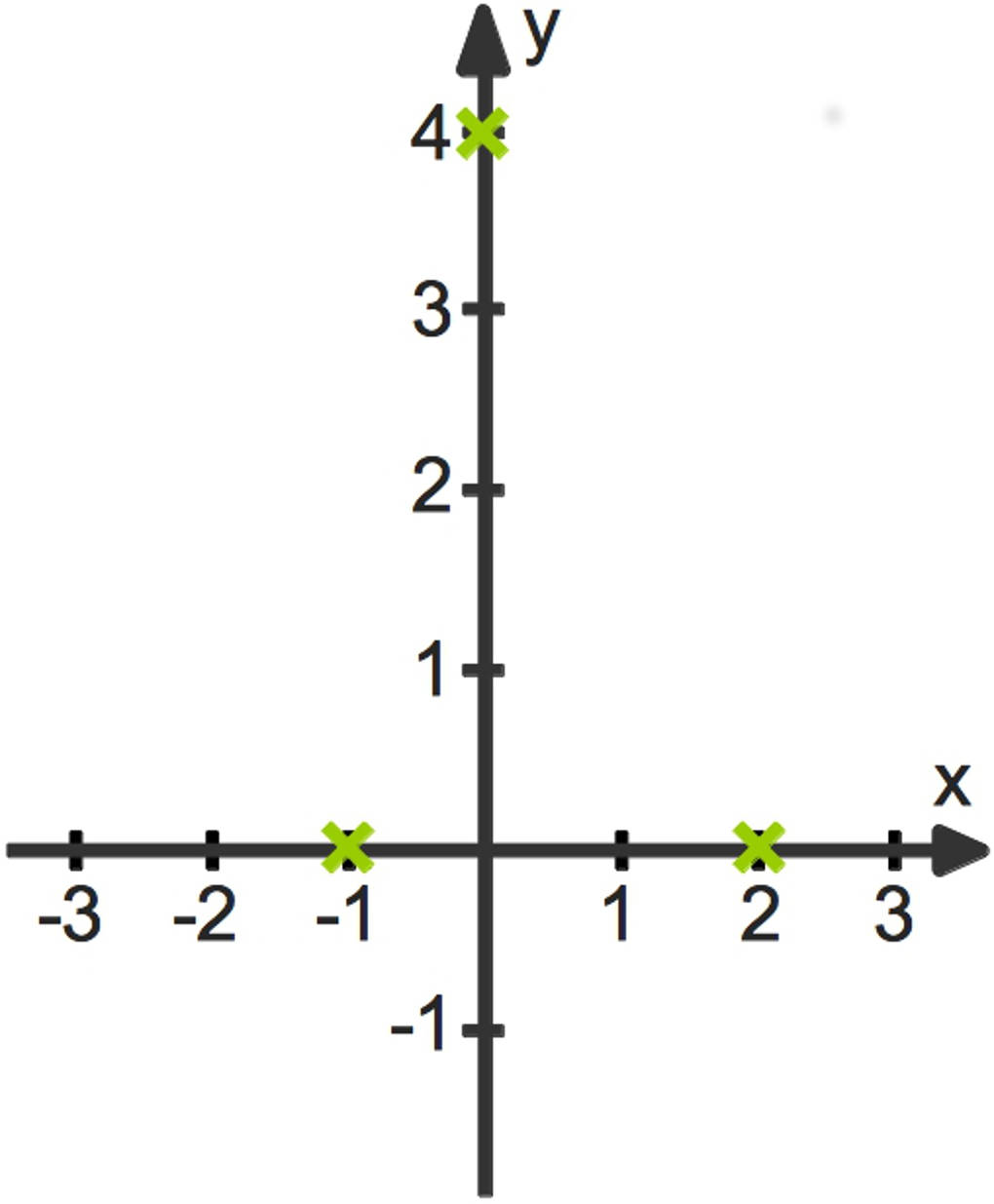
Nun können wir auch diese Punkte in das Koordinatensystem eintragen.

Monotonie

Die Monotonie kannst du mit der ersten Ableitung erklären. Diese steht für die Steigung einer Funktion.

• Links von einem Hochpunkt ist eine Funktion monoton wachsend ($f'(x)>0$) und rechts davon monoton fallend ($f'(x)<0$).
• Links von einem Tiefpunkt ist eine Funktion monoton fallend ($f'(x)<0$) und rechts davon monoton wachsend ($f'(x)>0$).

Vorzeichenwechselkriterium

Auch beim Vorzeichenwechselkriterium schaust du dir zunächst die Nullstellen der ersten Ableitung an. Diese sind $x_{E_1}=0$ und $x_{E_2}=2$.

In einem Extremum muss die erste Ableitung einen Vorzeichenwechsel haben.

Nun betrachtest du die erste Ableitung links und rechts von den Nullstellen. Dies kannst du hier exemplarisch für $x_{E_1}=0$ sehen:

• Die erste Ableitung $f'(x)=3x^2-6x$ ist eine quadratische Funktion mit einer nach oben geöffneten Parabel als Graph. Der Faktor vor $x^2$ ist positiv.
• Das bedeutet, dass links von $x_{E_1}=0$, der linken der beiden Nullstellen, die Funktionswerte der ersten Ableitung positiv und rechts davon negativ sind.
• Also liegt an der Stelle $x_{E_1}=0$ ein (lokaler) Hochpunkt vor.

Ebenso kannst du erklären, dass an der Stelle $x_{E_2}=2$ ein (lokaler) Tiefpunkt vorliegt. Die entsprechenden Punkte sind bereits oben angegeben.

Die Wendepunkte einer Funktion

Während die erste Ableitung für die Steigung einer Funktion steht, steht die zweite Ableitung für die Krümmung. Ein Wendepunkt ist ein Punkt des Funktionsgraphen, in welchem ein Krümmungswechsel geschieht. Dazu müssen wir die Nullstellen der zweiten Ableitung bestimmen.

• Die notwendige Bedingung für Wendepunkte lautet $f''(x)=0$. Also bei unserem Beispiel $6x-6=0$. Addition von $6$ und Division durch $6$ führt zu $x_W=1$.
• Die hinreichende Bedingung für einen Wendepunkt lautet, dass zusätzlich $f'''(x)\neq 0$ ist. Die dritte Ableitung ist hier $f'''(1)=6\neq 0$.
• Die Funktion hat also einen Wendepunkt $WP(1|2)$.

Auch diesen kannst du wieder in das Koordinatensystem eintragen.

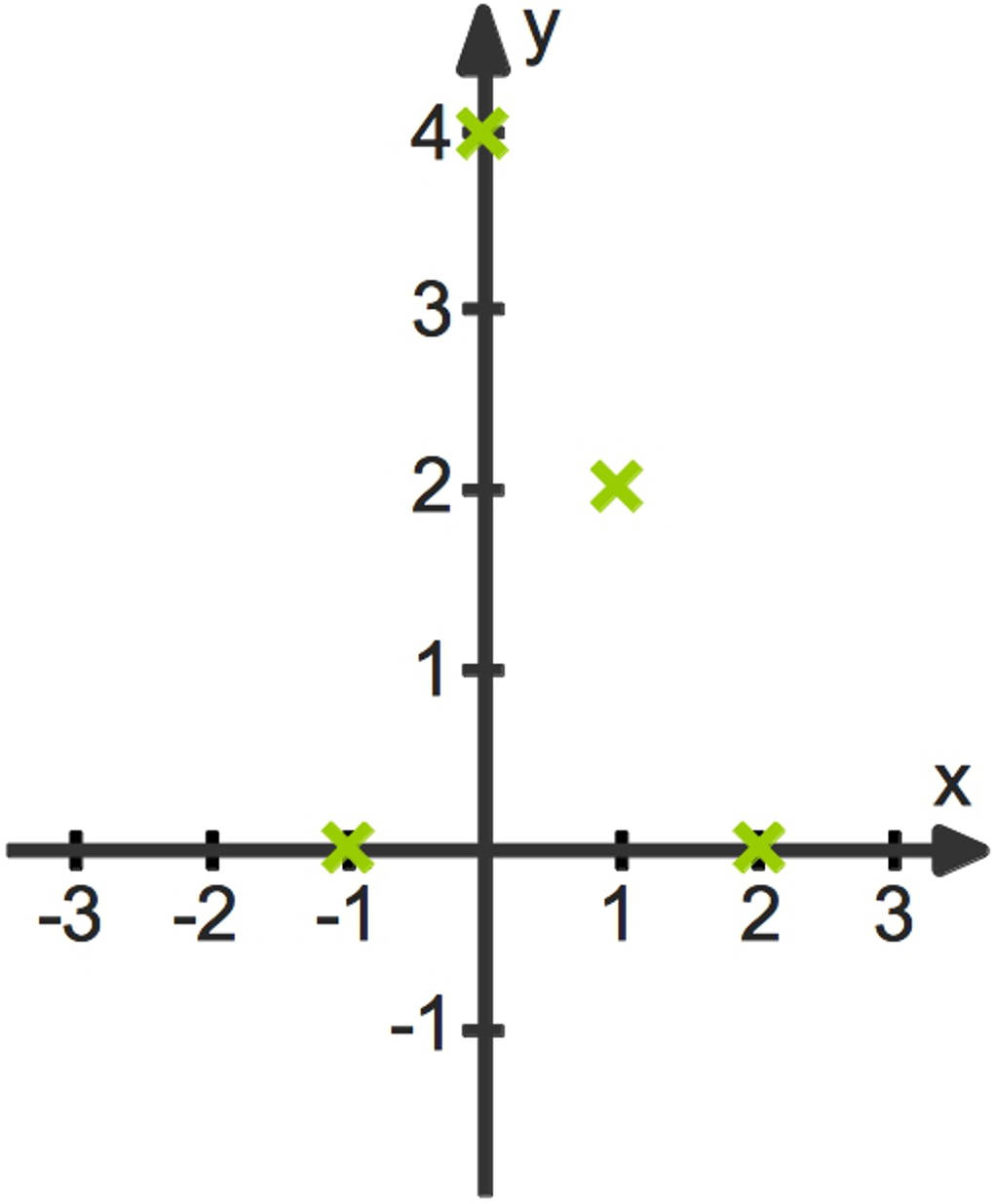
Wendepunkte mit waagerechter Tangente werden Sattelpunkte genannt.

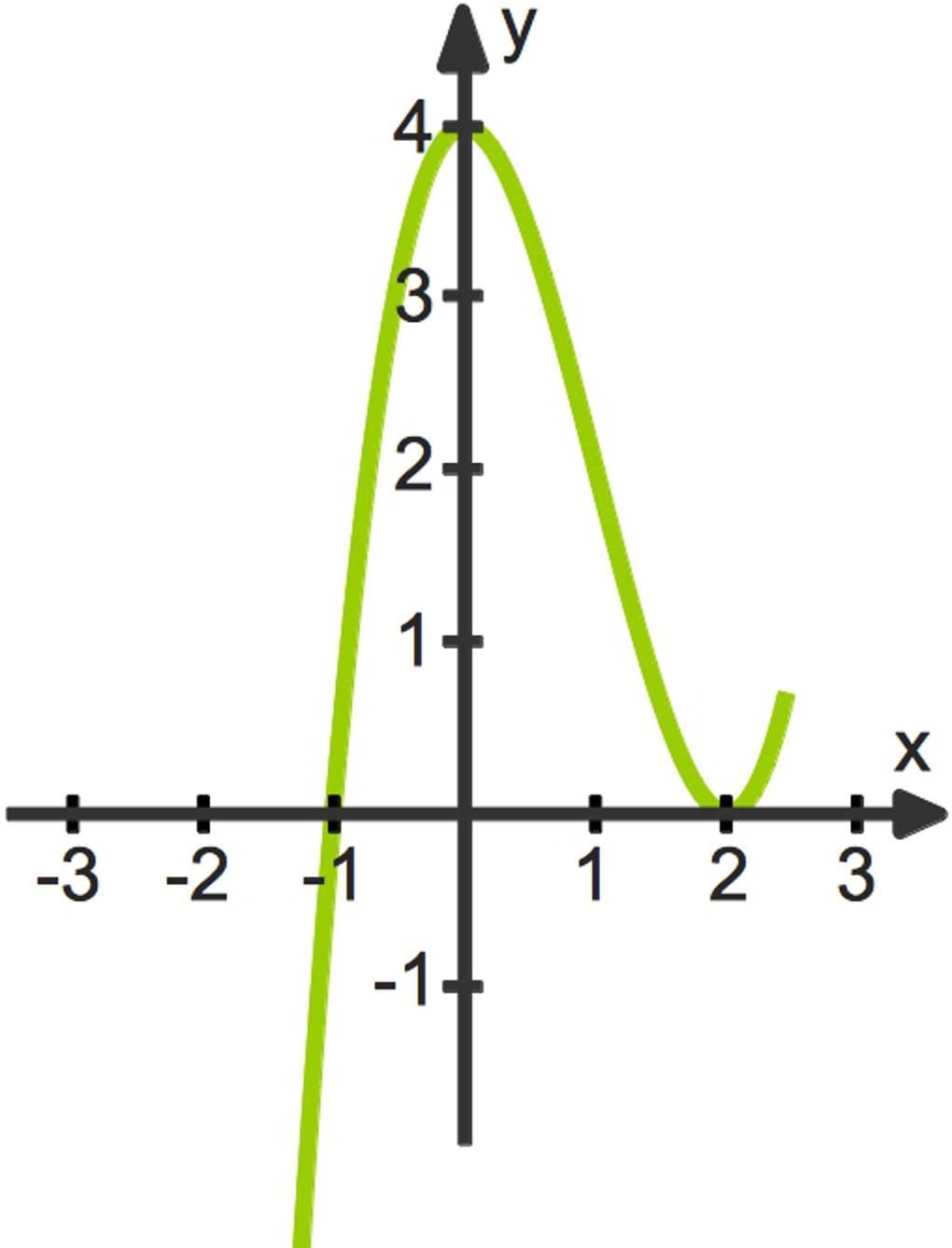
Der Graph einer Funktion

Wenn du mit allen obigen Schritten der Kurvendiskussion fertig bist, kannst du die gefundenen Punkte miteinander verbinden. Mit ein wenig Übung kannst du kubische Funktionsgraphen leicht zeichnen.